Systèmes linéaires continus invariants analyse frequentielle partie3

Sciences Indusrielles

Systèmes linéaires continus invariants

ANALYSE FREQUENTIELLE

SYSTEMES LINEAIRES CONTINUS

INVARIANTS

ANALYSE FREQUENTIELLE

3 Système du deuxième ordre.

3.1 Définition d’un système du deuxième ordre

Un système du second ordre a son compo rtement régi par une équation différentielle du deuxième ordre de la forme :

e = e (t) entréedusystème

s = s(t) réponsedusystèmeàl’entréee(t)

2x ds

+ s = Ke

K:gainstatique(>0)

w₀²

dt ²

w₀

^ïx :coefficient d’amortissement (sans dimension) (>0)

pulsationpropredusystème(enrads^-1 )

3.2 Fonction de transfert globale d’un deuxième ordre

On applique la transformée de Laplace à l’ensemble de l’équation différentielle ci-dessus, avec des conditions initiales nulles :

Donc :

1 d ² s

2x ds

+ s = Ke transforméedeLaplace

p²

S ( p) +

pS( p) + S ( p) = KE ( p)

w² dt ²

uuuuuuuuuuuuuuuuuuuuuuuuru _w 2

On peut alors présenter le rapport de la sortie S(p) sur l’entrée E(p), c’est à dire la fonction de

transfert globale du système :	H ( p) =	S( p)	=			K
transfert globale du système :	H ( p) =		=		2x		p²
		E ( p)		1+	2x	p +	p²
				1+	w₀	p +
					w₀		w₀	2

On notera :

Le gain statique vaut : K=H(0)
Pour identifier les caractéristiques d’un système du deuxième ordre (c’est à dire

K , x et w₀ ), on veillera bien à présenter la fonction de transfert globale H(p) avec le coefficient en p⁰ du polynôme au dénominateur égal à 1. Ainsi le numérateur peut être identifié au gain statique K, coefficient en p² du polynôme au dénominateur peut être identifié à l’inverse de la pulsation proprew₀ et on déduit l’amortissement du

coefficient en p¹ : ²^x .

w₀

Page 1 Emmanuel FARGES Ó EduKlub S.A.

Tous droits de l’auteur des œuvres réservés. Sauf autorisation, la reproduction ainsi que toute utilisation des œuvres autre que la consultation individuelle et privée sont interdites.

Sciences Indusrielles

Systèmes linéaires continus invariants

ANALYSE FREQUENTIELLE

3.3 Gain et phase réels d’un deuxième ordre

H ( jw) =

( jw )

–

+ j

2xw

jw +

ç¹

w₀

w₀ ²

w₀

w ₀

Calcul du gain :

H ( jw)

soit en dB :

H ( jw )

_dB = 20Log

H ( jw)

w²

4x ²w ²

÷ ⁺

w ²

w²

_w 2 _ö²

4x ² w²

H ( jw)

= 20LogK – 20Log _ç1

–

w₀

Existence d’une résonance :

Il existe une résonance si il existe une pulsation w_r

dite pulsation de résonance pour laquelle

w ² ö

4x ² w²

le gain

H ( jw)

_dB = 20LogK – 20Log

ç¹

–

présente un maximum.

w₀

Le gain est maximum si la fonction de w :

w² ö

4x ² w²

est minimale :

w₀

Etude de cette fonction : Posons x =

w²

w ² ö

4x ² w²

, alors la fonction :

f (w ) = _ç 1-

est

w₀

w ₀

w₀

minimale si la fonction : g( x) = (1- x)² + 4x ² x = 1+ (4x²

– 2)x + x² est minimale .

g¢( x) = 4x ² – 2 + 2x , donc on a un extremum pour x telque g ¢(x) = 0 , c’est à dire pour

= 1- 2x ² .


Donc la pulsation pour laquelle on a résonance est :	w = w	0	1 – 2x ²
	r	0

Remarque : On voit donc bien que la résonance ne peut exister que dans certains cas d’amortissement (terme sous la racine positif).

On a résonance pour des valeurs d’amortissement : x < ² 2

Quantification de la résonance : facteur de surtension Q

Le facteur de surtension exprimé en dB est la différence entre la valeur du pic de résonance et le gain statique : Q_dB = H ( jw_r ) _dB– 20LogK

w²

4x ²w ²

H ( jw

)

– 20LogK = -20Log

–

w₀

Q_dB = -20Log (1 – (1- 2x ² ))²

+ 4x ² (1- 2x ² )

			(				)
Q = -20Log	4x ⁴ + 4x ² -8x ⁴ = -20Log 4x ² – 4x ⁴ = – 20Log		(	2x	1- x ²		)
dB
Page 2		Emmanuel FARGES				Ó EduKlub S.A.

Tous droits de l’auteur des œuvres réservés. Sauf autorisation, la reproduction ainsi que toute utilisation des œuvres autre que la consultation individuelle et privée sont interdites.

Sciences Indusrielles

Systèmes linéaires continus invariants

ANALYSE FREQUENTIELLE

D’où le résultat final :

^QdB

= 20Log

Or Q est tel que

^QdB

= 20L o g Q

, donc :

(2x

1 –x ² )

Q =

(2 x

1- x ²

)

Calcul de la phase :

(w ) = Arg [ H ( jw)]

é æ

w ² ö

2xw ^ù

H ( jw) =

ê ç¹ ^–

_÷ – j

_ú , donc :

w ² ö

2xw

ç¹

–

÷ ⁺

^æ1-

ë è

w₀

é æ

w² ö

2xw ù

j (w ) = Arg [H( jw) ] = Arg ê _ç 1

–

_÷ – j

w₀

ë è

w₀

ææ

–

w ²

– j

2xw ö

ææ

1 –

w²

– j

2xw ö

æ æ

w²

– j

2xw ö

Im ç 1

Re ç

Im ç

ç^ç

tan j =

èè

w₀

^w0 ø

;cosj =

w₀

^w0 ø

;sin j =

w ₀

^w0 ø

æ æ

–

w²

– j

2xw ö

–

w ²

– j

2xw

w²

– j

2xw

Re ç 1

w²

w ²

ç ^ç

è è

0 ø

– 2xw

^æ1-

w ²

-2xw

w₀

Donc :

tan j =

;cosj =

w₀

;sinj =

^æ1 –

ö ₊

2 2

4x w

^w0 ø

w ²

w²

w₀

2xw

w₀

j (w) = – arctan ^ê

w²

ê _æ

–

ö^ú

ç ¹

÷ú

w₀

øû

3.4 Asymptotes des diagrammes de Bode

Deux méthodes sont possibles pour déterminer les asymptotes des diagrammes de Bode : Soit on détermine les équivalents en 0 et en +¥ du gain réel et de la phase réelle, soit on cherche des équivalents directement sur la fonction de transfert.

1^ère méthode : équivalents à partir des fonctions de gain et de phase réels.

Asymptote sur le diagramme de gain :

w ²

4x ² w²

H ( jw)

_dB = 20LogK – 20Log

ç¹

–

est la fonction du gain (en dB) réelle

w₀

Ó EduKlub S.A.

Page 3

Emmanuel FARGES

Tous droits de l’auteur des œuvres réservés. Sauf autorisation, la reproduction ainsi que toute utilisation des œuvres autre que la consultation individuelle et privée sont interdites.

Sciences Indusrielles

Systèmes linéaires continus invariants

ANALYSE FREQUENTIELLE

Ø équivalent lorsque w ® 0 : on peut négliger les termes en w ² et w⁴				devant1.Donc :

	H ( jw)	; 20LogK	, c’est une droite horizontale d’ordonnée	20LogK dB.
		{
		^dB w ® 0

équivalent lorsque w ® ¥ : on peut négliger le terme en

H ( jw)

;

20LogK – 20Log

w⁴

{

1et w ² devant celuien w⁴ .Donc :

^dB w ® ¥

w₀

;

20LogK + 20Logw² – 20Logw²

{

w ® ¥

soit, mis en forme différemment pour faire clairement apparaître la pente de la droite :

H ( jw)

; 20 LogK + 40Logw

-40

Logw

c’est une

{

^dB w ® ¥

pente d e l a d r o iteasymptote

Logw₀ ) .

droite de pente -40 ^dB

décade

passant par le point (w = 1;

20LogK + 40

Intersection entre les deux asymptotes :

On cherche la pulsation dite pulsation propre du système notée w _p pour laquelle les deux asymptotes ont des valeurs égales. L’équation permettant de déterminer w _p est donc :

20LogK = 20LogK + 40Logw ₀ – 40Logw _p .

Soit 40Logw _p = 40Logw₀ ; d’où :w _p = w₀

Asymptote sur le diagramme de phase :

La fonction de phase réelle est définie par

– 2xw

^æ1-

w ²

-2xw

w₀

tan j =

;cosj =

w₀

;sinj =

2 2

^æ1 –

2 2

–

4x w

^w0 ø

w ²

w²

w₀

2xw

w₀

j (w) = – arctan

w²

ê _æ

–

ö^ú

ç ¹

÷ú

w₀

øû

Ø équivalent lorsque w ® 0 : tan j ® 0

; cosj ® 1

;

sin j ® 0 .Donc,

{

w®0

w ®0

w®0

j (w)

0° on a une asymptote horizontale à 0°

{

w ® 0

Page 4 Emmanuel FARGES Ó EduKlub S.A.

Tous droits de l’auteur des œuvres réservés. Sauf autorisation, la reproduction ainsi que toute utilisation des œuvres autre que la consultation individuelle et privée sont interdites.

Sciences Indusrielles

Systèmes linéaires continus invariants

ANALYSE FREQUENTIELLE

Ø équivalent lorsque w ® ¥ : tan j ® 0 ; cosj ® – 1 ; sinj ® 0^– .Donc,

{ { {

w®¥ w ®¥ w®¥

j(w ) » –p (- 180°) (car le cosinus tend vers -1 et le sinus vers 0 par valeurs

{

® ¥

négatives) on a une asymptote horizontale à -180°

	æ	ö		(		= – arctan (+¥) = –	p	(- 90°)
Comme	j ç w	÷	= j		w	= – arctan (+¥) = –	2	(- 90°)	, on relie les deux asymptotes qui
	è	p _ø			0 ⁾		2

sont normalement parallèles (puisque toutes les deux horizontales) au niveau de la pulsation propre du système w _p = w₀ .

2^ème méthode : équivalents à partir de la fonction de transfert :

On cherche des équivalents de la fonction de transfert de la forme

pⁿ

Fonction de transfert équivalente pour w ® 0 , c’est à dire pour p ® 0 (puisque p = jw )

H ( p) =

équivalent à

soit

p²

14243

p +

quand p ® 0

On retrouve donc l’asymptote horizontale pour w ® 0 à 20LogK pour la courbe de gain en dB (d’après les résultats démontrés paragraphe 1.3.3)
On retrouve donc l’asymptote horizontale pour w ® 0 à 0° pour la courbe de phase (d’après les résultats démontrés paragraphe 1.3.3)

Fonction de transfert équivalente pour w ® ¥ , c’est à dire pour p ® ¥ (puisque p = jw )

H ( p) =

équivalentà

K w₀²

p +

14243

quand p ® ¥

w ₀

w₀

On retrouve donc l’asymptote de pente -40dB/décade pour w ® ¥ à

20LogKw₀² – (20 ´ 2) Logw = 20LogK + 40Logw₀ – 40Logw pour la courbe de gain en dB (d’après les résultats démontrés paragraphe 1.3.3)

ü On retrouve donc l’asymptote horizontale pour w ® ¥ à –p (- 180°) pour la courbe de phase (d’après les résultats démontrés paragraphe 1.3.3)

Page 5 Emmanuel FARGES Ó EduKlub S.A.

Tous droits de l’auteur des œuvres réservés. Sauf autorisation, la reproduction ainsi que toute utilisation des œuvres autre que la consultation individuelle et privée sont interdites.

Sciences Indusrielles

Systèmes linéaires continus invariants

ANALYSE FREQUENTIELLE

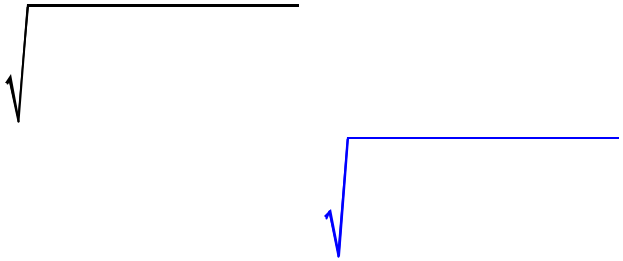
Graphiquement cela donne les diagrammes asymptotiques schématiques suivants :

Systèmes linéaires continus invariants

20LogK	H	dB	(w)	*Pente :* -40 dB / décade
	H		(w)	*Pente :* -40 dB / décade

					*Ecart de 40dB*
					w
	w _p = w₀			*1 décade*	10w₀

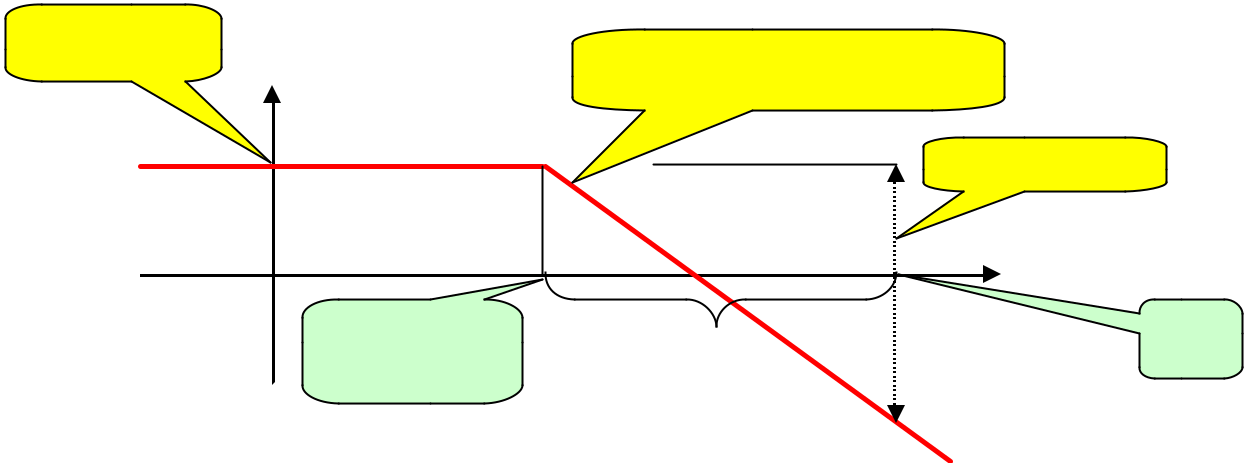
(w )

0°	w _p	= w₀

-180°

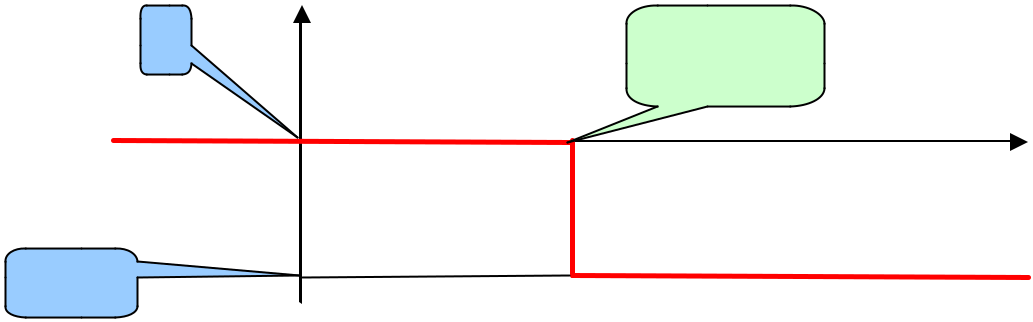
3.5 Diagrammes de Bode d’un deuxième ordre

H _dB (w)

Asymptote horizontale à

20LogK

1 décade

Asymptote de pente -40 dB /décade et d’équation

20LogK + 40Logw ₀ – 40Logw

Gain du deuxième ordre (K=10 , x =0,1 et w₀ = 10rads^-1) Avec résonance : x = 0,1 Þ Q_dB ; 14dB

Gain du deuxième ordre (K=10 , x =0,5 et w₀ = 10rads^-1).Avec résonance : x = 0,5 Þ Q_dB =1,25dB

Gain du deuxième ordre (K=10 , x =0,9 et w₀ = 10rads^-1) sans résonance

Gain du deuxième ordre (K=10 , x =2 et w₀ = 10rads^-1) sans résonance

w (rad s^-1 )

Pulsation propre w₀

Page 6 Emmanuel FARGES Ó EduKlub S.A.

Tous droits de l’auteur des œuvres réservés. Sauf autorisation, la reproduction ainsi que toute utilisation des œuvres autre que la consultation individuelle et privée sont interdites.

Sciences Indusrielles

Systèmes linéaires continus invariants

ANALYSE FREQUENTIELLE

j (w ) ici

en degré

Asymptote horizontale à 0°

j (w₀ ) = -arctan ¥ = – = -90°

-180°

Phase du deuxième ordre (K=10 , x =0,1 et w₀ = 10rads^-1)

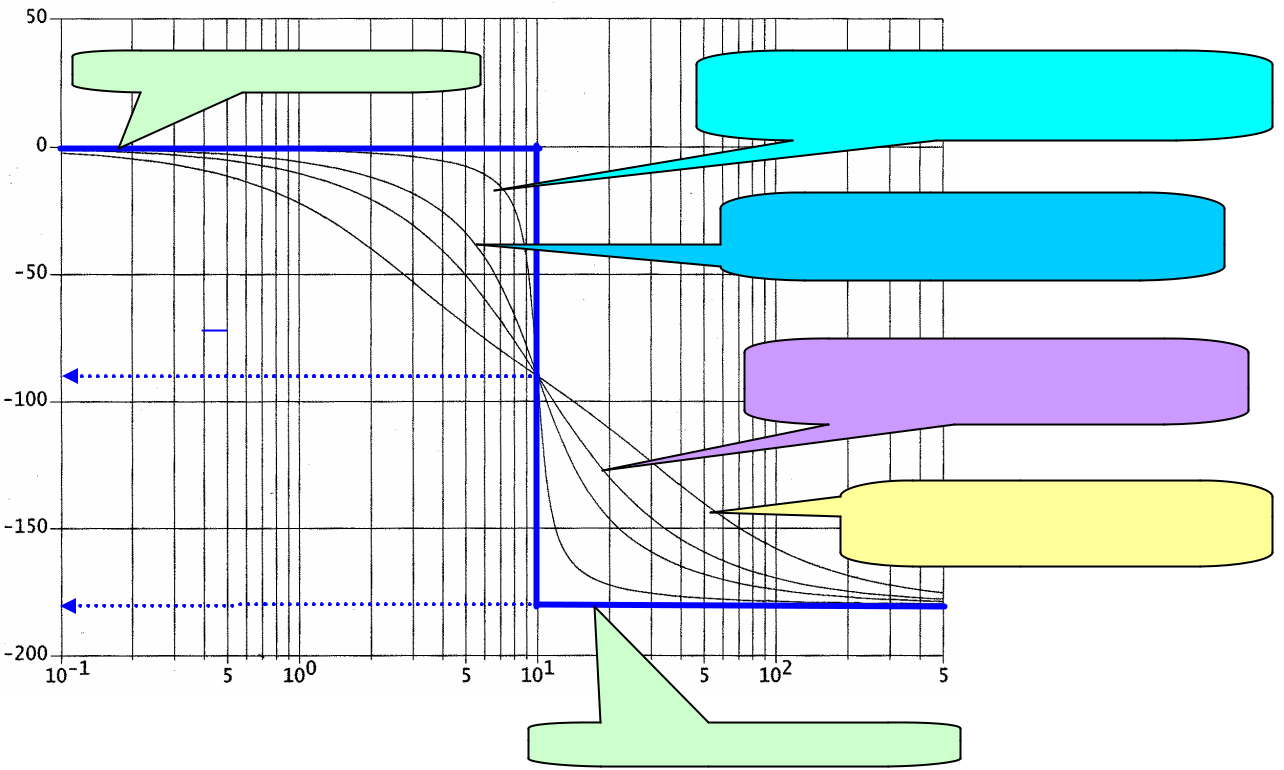
Phase du deuxième ordre (K=10 ,

=0,5 et w₀ = 10rads^-1).

Phase du deuxième ordre (K=10 ,

=0,9 et w₀ = 10rads^-1)

Phase du deuxième ordre

(K=10 , x =2 et w₀ = 10rads^-1)

w (rad s^-1 )

Asymptote horizontale à -180°

Construction des courbes de Bode asymptotiques d’un système de fonction de transfert quelconque.

4.1 Diagrammes de Bode de l’inverse d’une fonction de transfert

Considérons un système de fonction de transfert H ( p ) =	1	avec	H ₁( p) une fonction de

	H ₁ ( p )
transfert dont on connaît les diagrammes de Bode.

Peut on déduire les diagrammes de Bode de H ( p) connaissant ceux de H ₁( p) ?
On pose j (w ) et H _dB (w) respectivement la phase et le gain en dB de			H ( p)
On pose j₁ (w ) et H₁_dB (w) respectivement la phase et le gain en dB de				H ₁( p)
On cherche donc à trouver une relation entre j (w ) et j₁ (w ) , puis entre				H _dB (w) et H₁_dB (w)

^jj⁽^w⁾

On peut écrire le complexe H ( jw) sous sa forme exponentielle : H ( jw ) = H ( jw) e

^jj⁽^w⁾

On peut écrire le complexe H ₁( jw) sous sa forme exponentielle : H₁ ( jw ) = H₁ ( jw) e ¹

Donc

H ( jw)

_e jj (w ) ₌

_e^– ^jj 1 (^w ) _.

jj₁ (w )

H₁ ( jw)

D’où :

H ( jw)

j (w) = –j₁ (w ) soit encore :

H ₁ ( jw)

H _dB (w ) = 20Log

= –H₁_db (w )

H( jw)

= 20Log ç

÷ = -20Log

H₁ ( jw )

( jw)

Ó EduKlub S.A.

Page 7

Emmanuel FARGES

Tous droits de l’auteur des œuvres réservés. Sauf autorisation, la reproduction ainsi que toute utilisation des œuvres autre que la consultation individuelle et privée sont interdites.

Sciences Indusrielles

Systèmes linéaires continus invariants

ANALYSE FREQUENTIELLE

_{Finalement :} ^ìï_í^H dB (^w ) ^{= –}^H1 dB (^w )

ï_î j (w ) = –j₁ (w )

Ce qui revient graphiquement à effectuer la symétrie de la courbe de gain par rapport à l’axe 0dB et la symétrie de la courbe de phase par rapport à l’axe 0°.

Application : Voit TD

4.2 Diagrammes de Bode d’un produit de fonctions de transfert

Diagrammes de Bode d’un produit de deux fonctions de transfert :

Considérons un système de fonction de transfert H ( p) = H₁ ( p)H ₂ ( p) avec H ₁( p) et H ₂ ( p) deux fonctions de transfert dont on connaît les diagrammes de Bode.

On pose j (w ) et H _dB (w) respectivement la phase et le gain en dB de H ( p)

On pose j₁ (w ) et H₁_dB (w) respectivement la phase et le gain en dB de H ₁( p)

On pose j ₂ (w) et H ₂ _dB (w) respectivement la phase et le gain en dB de H ₂ ( p)

Peut on déduire les diagrammes de Bode de H ( p) connaissant ceux de H ₁( p) et H ₂ ( p) ?

^jj⁽^w⁾

On peut écrire le complexe H ( jw) sous sa forme exponentielle : H ( jw ) = H ( jw) e

^jj⁽^w⁾

On peut écrire le complexe H ₂ ( jw) sous sa forme exponentielle : H ₂ ( jw ) = H ₂ ( jw) e ²

H ( jw) = H₁ ( jw )H ₂ ( jw) soit :

_H₍_jw₎ _e^jj (^w ) ₌ _H₁ ₍_jw₎ _e^jj1 (^w ) _H₂ ₍_jw₎ _e^jj 2 (^w )

j éj (w ) +j (w )ù

= H₁ ( jw ) H ₂ ( jw ) e ^ë ¹ ² ^û

Donc : H ( jw ) = H₁ ( jw ) H ₂ ( jw ) et j (w) = j₁ (w)+ j ₂ (w) , soit :

H _dB (w ) = 20Log H ( jw ) = 20Log ^é_ë H₁ ( jw ) H ₂ ( jw ) ^ù_û

20Log H₁ ( jw ) + 20Log H₂ ( jw ) = H₁ _dB (w ) + H₂ _dB (w )

Finalement :	ìH	dB (	w	)	= H	w	H	2 dB (	w	)
Finalement :	í^ï	dB (		)		1 dB ( )		2 dB (		)
	ï j (w ) = j₁ (w ) +j ₂ (w )
	î

Ce qui revient graphiquement à « sommer » les deux courbes de gain en dB et les deux courbes de phase.

Application : Voir TD

Page 8 Emmanuel FARGES Ó EduKlub S.A.

Tous droits de l’auteur des œuvres réservés. Sauf autorisation, la reproduction ainsi que toute utilisation des œuvres autre que la consultation individuelle et privée sont interdites.

Sciences Indusrielles

Systèmes linéaires continus invariants

ANALYSE FREQUENTIELLE

4. 3 Diagrammes de Bode d’un système de fonction de transfert quelconque

Le but est d’écrire cette fonction de transfert quelconque sous forme d’un produit de fonction de transfert connues (1^er ordre, 2^ème ordre, intégrateur ou dérivateur simple ou multiple :

H ( p) = _pa ) pour pouvoir ensuite « sommer » les courbes connues.

On obtiendra ainsi un maximum d’équivalents successifs intermédiaires pour les diagrammes de Bode asymptotiques qui s’approche donc ainsi un peu plus du diagramme réel

Page 9 Emmanuel FARGES Ó EduKlub S.A.

Tous droits de l’auteur des œuvres réservés. Sauf autorisation, la reproduction ainsi que toute utilisation des œuvres autre que la consultation individuelle et privée sont interdites.

Telecharger