Blog

Réseaux de Neurones – Introduction:

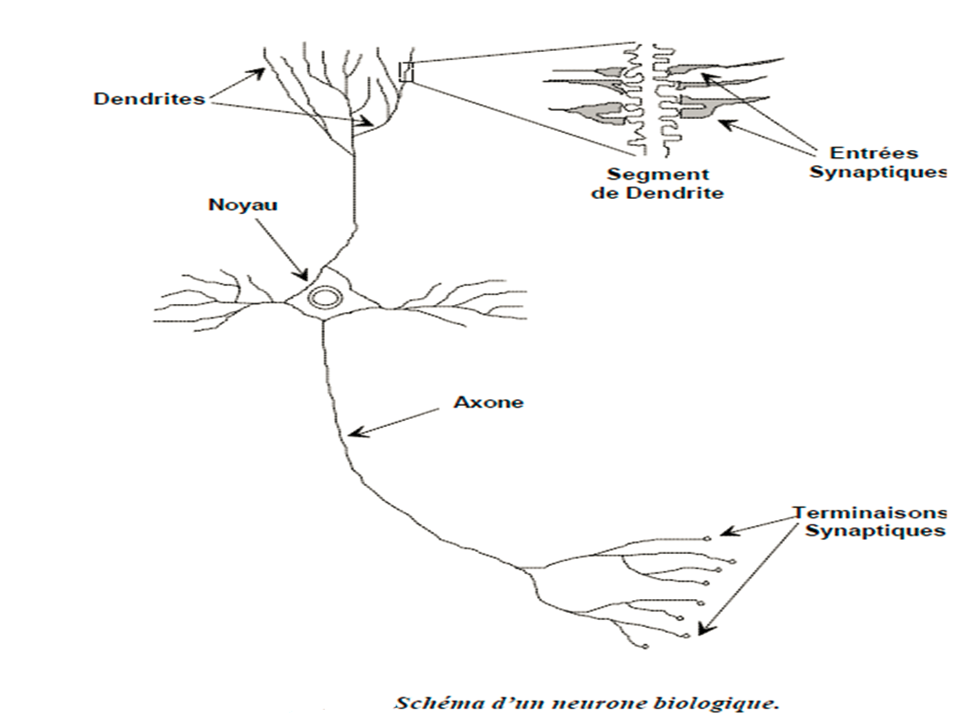
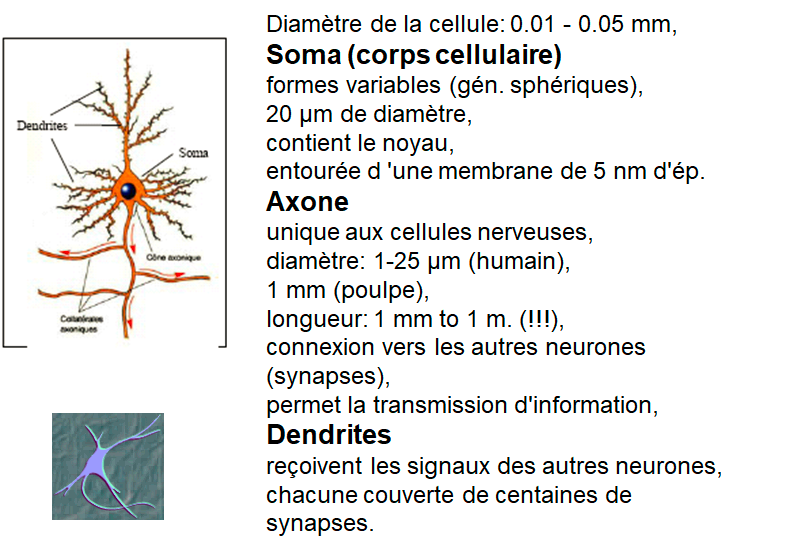
Un réseau de neurones ou Neural Network est un système informatique s’inspirant du fonctionnement du cerveau humain (des neurones biologiques).

Un réseau neuronal s’inspire du fonctionnement des neurones biologiques et prend corps dans un ordinateur sous forme d’un algorithme. Le réseau neuronal peut se modifier lui-même en fonction des résultats de ses actions, ce qui permet l’apprentissage et la résolution de problèmes sans algorithme.

Quelques chiffres …

• Nombre de neurones dans le cerveau: ~ 10¹¹   (100 milliards)

• Nombre de connexions par neurone: ~ 10⁴ – 10⁵

• Temps de cycle (switching time): ~ 10^-3 seconde

• Temps moyen d’une activité cognitive: ~ 0.1 seconde

(ex. reconnaissance de visages)

Il n’y a donc de la place que pour 100 cycles de traitement, ce qui est insuffisant pour une activité complexe !!!

Le cerveau doit donc effectuer des opérations en parallèle !!!

Modélisation Réseaux de Neurones

• Intuition

– les capacités (intelligence?) résident dans les connexions entre les milliards de neurones du cerveau humain.

• Propriétés d’une modélisation

  – neuro-biologiquement logique (unité ≈ neurone),

  – traitement distribué et parallélisme massif

    • • beaucoup d’interconnexions entre unités,

   • • ajustement automatique des poids des connexions,

Le terme « réseaux de neurones » peut prendre des significations différentes:

– réseaux de neurones artificiels,

– modèles connexionnistes,

– neurosciences calculatoires,

– modélisation neuronale.

Les réseaux de neurones artificiels (RNA)

Depuis plusieurs années, les réseaux de neurones artificiels, et particulièrement les perceptrons multicouches, se sont montrés très efficaces dans le domaine de la reconnaissance statistique de formes. Ces systèmes sont composés d’un ensemble structuré d’unités de traitement, appelées neurones, qui fonctionnent en parallèle et qui sont fortement interconnectées.

  Ces neurones réalisent chacun une fonction non linéaire de leurs entrées, qui est déterminée par un ensemble de paramètres dont les valeurs sont établies à la suite d’un apprentissage par l’exemple. Les non-linéarités présentes dans ces systèmes connexionnistes, ainsi que l’apprentissage discriminant qu’ils subissent, rendent ces derniers particulièrement bien adaptés aux tâches de classification.

Réseau de neurones en informatique

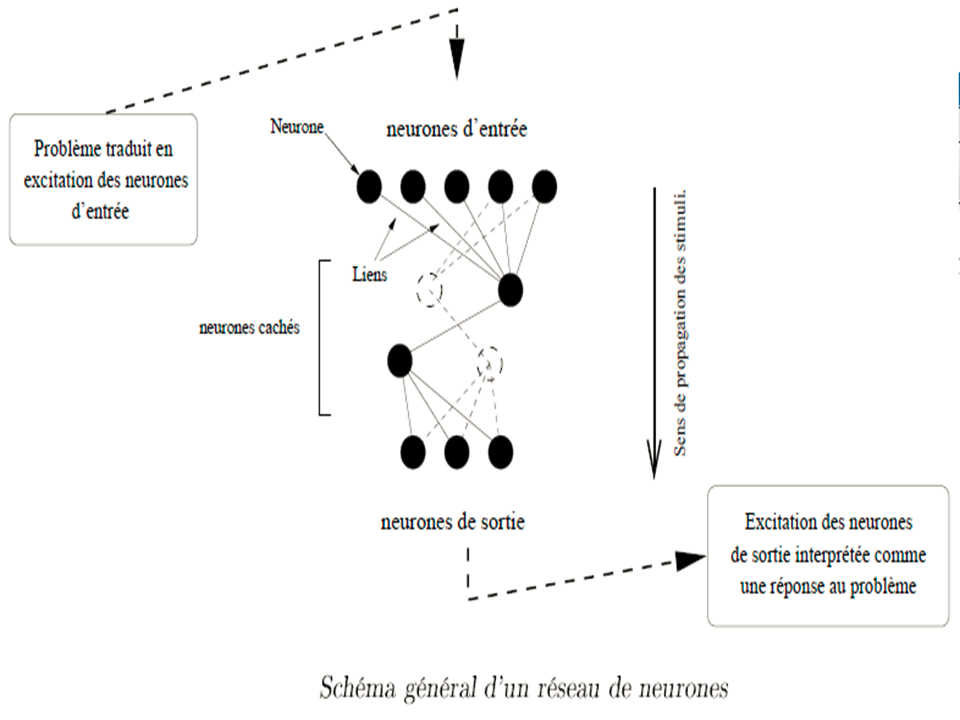
• En informatique, on appelle réseau de neurones un ensemble d’entités (les neurones) interconnectés.
• Dans la grande majorité des cas, les neurones sont en fait des fonctions calculés par un programme informatique, mais il sont parfois sur des circuits électroniques.
• Les neurones sont caractérisés par un état d’excitation qui dépend de celui des neurones situés en amont, ainsi que des liens qui les relient.

Modèle non-linéaire

(version actuelle du modèle de McCulloch & Pitts)

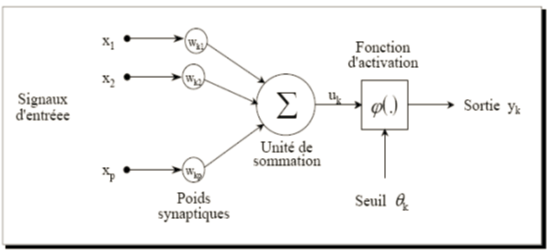
Ce modèle est mathématiquement décrit par 2 équations:

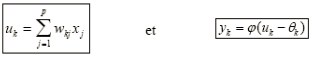
où:

x₁, x₂, …, x_p sont les entrées,

w_k1, w_k2, …, w_kp sont les poids synaptiques du neurone k,

u_k est la sortie de l’unité de sommation,

Θ_k est le seuil,

ϕ(.)est la fonction d’activation,

y_k est le signal de sortie du neurone k.

Modèle étendu

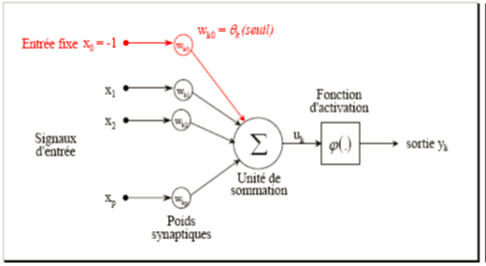
La fonction d’activation définit la valeur de sortie d’un neurone en termes des niveaux d’activité de ses entrées.

3 types de fonctions d’activation :

Topologies de réseaux

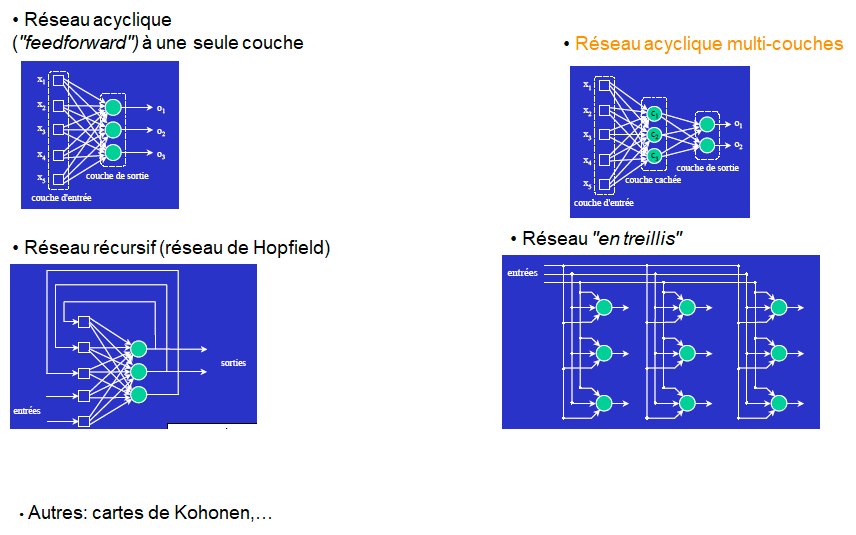
Le modèle « Perceptron »

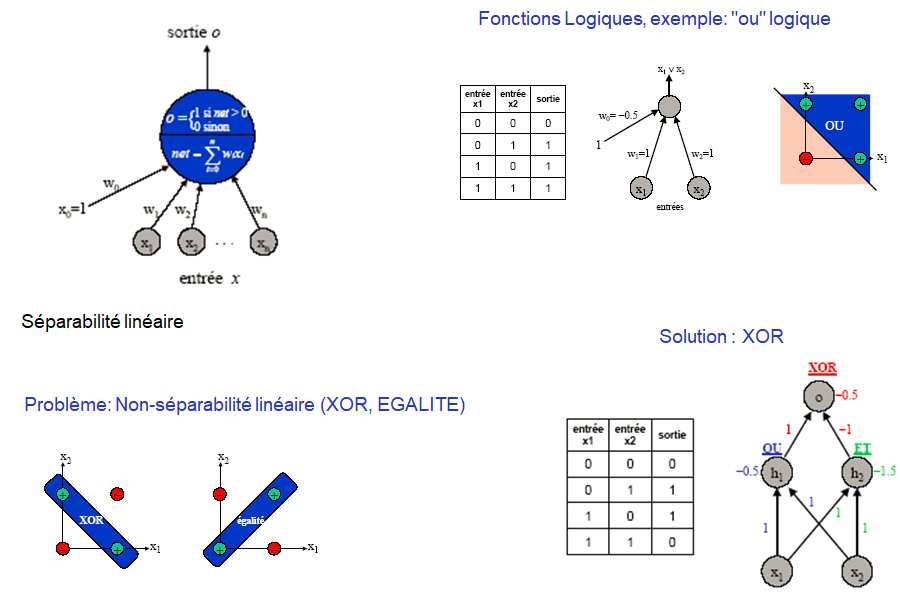
Théorème d’apprentissage (F. Rosenblatt)

Étant donné suffisamment d’exemples d’apprentissage, il existe un algorithme qui apprendra n’importe quelle fonction linéairement séparable.

Càd :  trouver les poids w_k /

w₀ + w₁*x₁+ w₂*x₂ + ….. + w_n*x_n = 0

Equation d’un hyperplan

Algorithmed’apprentissage du Perceptron (correction d’erreur)

Entrées: ensemble d’apprentissage {(x₁,x₂,…,x_n,t)}

Méthode

initialiser aléatoirement les poids w(i), 0<=i<=n

  répéter jusqu’à convergence:

  pour chaque exemple

  calculer la valeur de sortie o du réseau.

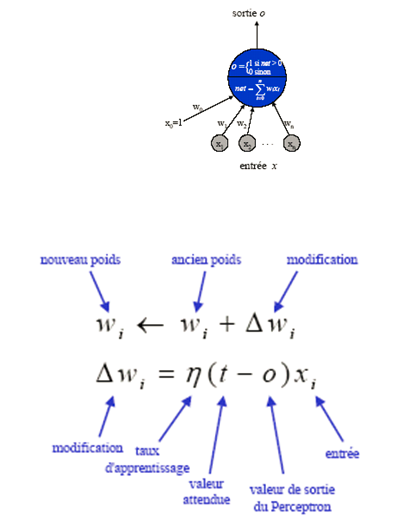
  ajuster les poids:

  ∆w_i = η(t – o) x_i

  w_i ←w_i + ∆w_i   

Règle d’apprentissage du Perceptron ( WIDROW-HOFF)

EXEMPLE

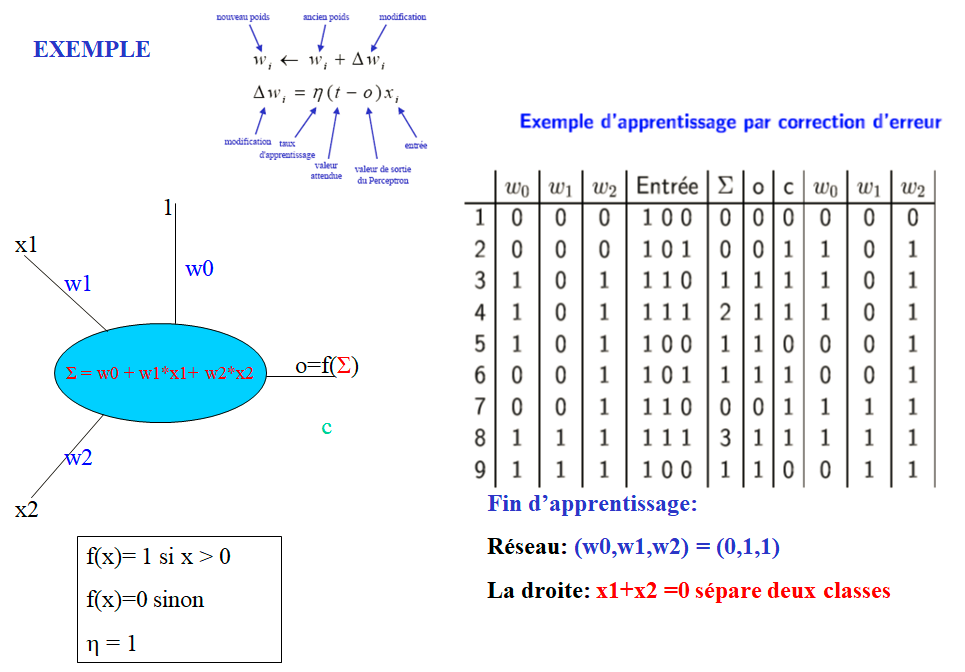
Conclusion

A partir d’un modèle simple des neurones biologiques, on a construit un modèle plus complexe, celui des perceptrons multi-couches. Ces outils permettent de calculer des fonctions vectorielles, adaptables à un ensemble d’exemples par le biais d’algorithmes d’optimisation utilisant la technique de la rétro-propagation. De cette façon, on peut espérer faire apprendre une fonction complexe à un MLP simple, contenant assez peu de neurones. On obtiendra ainsi une modélisation analytique compacte d’une fonction obtenue expérimentalement. 

EXERCICE 1

Considerez le perceptron et l’echantillon suivant :

Question 1:  Donnez des valeurs aux poids w0,w1,w2 et w3 de sorte que le perceptron classie correctement l’echantillon. (w0 = ?, w1 = ?, w2 =?,  w3 =?)

Question 2 : Donnez des valeurs aux poids w0,w1,w2 et w3 de sorte que le perceptron classie correctement l’echantillon inverse

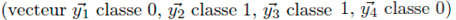
(w0 = ?, w1 = ?, w2 =?,  w3 =?)

Considérons l’éechantillon  suivant:

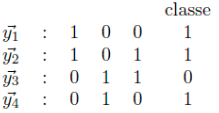
Question 3 Si on applique l’algorithme d’apprentissage par correction d’erreur en commencant par le vecteur w = (0, 0, 0, 0) on obtient le vecteur de poids (a quatre dimensions, le premier pour le seuil) suivant : ?

Exercice 2

On considere un perceptron special avec trois entrees x₁ x₂, et x3, trois poids w₁, w₂ et w₃ et deux seuils q₁ et q₂. La sortie de ce perceptron special est q₁, si  q₁ < w₁x₁+w₂x₂+w₃x₃ <q₂ et 0 sinon.

Question 4 : Donnez w₁, w₂, w₃, q₁ et q₂ de sorte que le perceptron classifie correctement l’echantillon suivant:

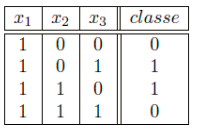
Réseaux multi-couches

• Un réseau à 2 couches (une couche cachée) avec des unités à seuil peut représenter la fonction logique « ou exclusif » (xor).

• Les réseaux multi-couches « feedforward » peuvent être entraînés par rétro-propagation pour autant que la fonction de transition des unités soit différentiable (les unités à seuil ne conviennent donc pas).

• Il faut apprendre les valeurs des poids w_iqui minimisent l’erreur quadratique

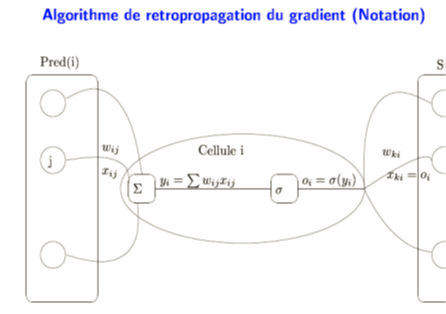
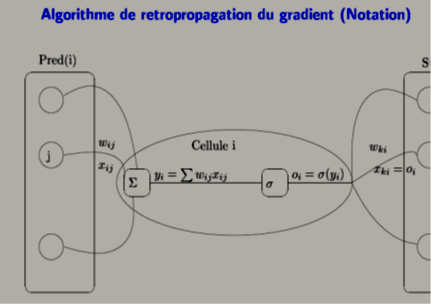
Exemple

Intelligence Artificielle   Apprentissage 

Trouver les nouveaux poids du réseau de la figure ci-dessous si on présente le vecteur d’apprentissage (0,1) (réf. Fausett, Prentice Hall, 1994)

1. Net de la couche cachée

z_in₁ = 0.4 + (0.0) (0.7) + (1.0) (-0.2) = 0.2

z_in₂ = 0.6 + (0.0) (-0.4) + (1.0) (0.3) = 0.9

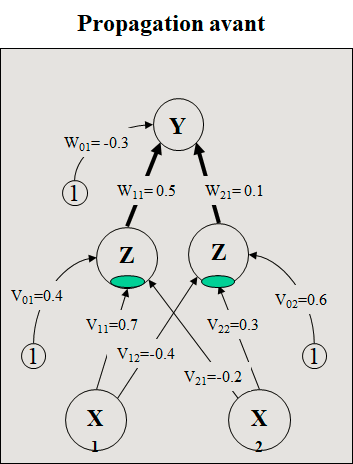
Trouver les nouveaux poids du réseau de la figure ci-dessous si on présente le vecteur d’apprentissage (0,1). a=1 et h=0,25.

2. Out de la couche cachée

z₁ = 1 / (1+ exp (- z_in₁)) = 0.550

z₂ = 1 / (1+ exp (- z_in₂)) = 0.711

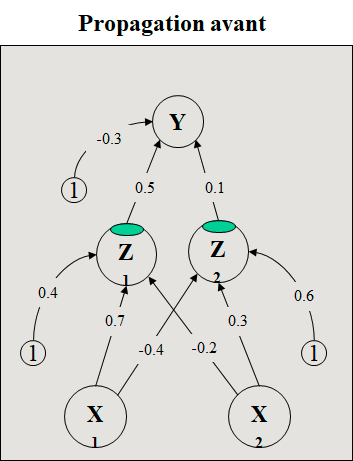
Trouver les nouveaux poids du réseau de la figure ci-dessous si on présente le vecteur d’apprentissage (0,1). a=1 et h=0,25.

3. Net de la couche de sortie

y_in = -0.3 + (z₁) (0.5) + (z₂) (0.1) = 0.046

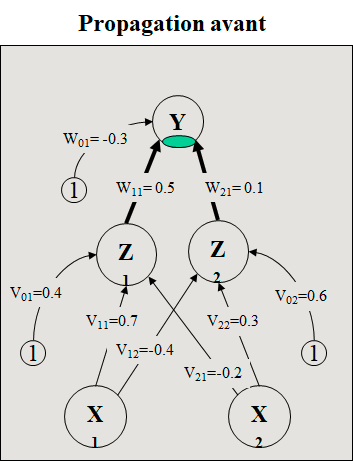
Trouver les nouveaux poids du réseau de la figure ci-dessous si on présente le vecteur d’apprentissage (0,1). a=1 et h=0,25.

1. Net de la couche cachée

z_in₁ = 0.4 + (0.0) (0.7) + (1.0) (-0.2) = 0.2

z_in₂ = 0.6 + (0.0) (-0.4) + (1.0) (0.3) = 0.9

2. Out de la couche cachée

z₁ = 1 / (1+ exp (- z_in₁)) = 0.550

z₂ = 1 / (1+ exp (- z_in₂)) = 0.711

3. Net de la couche de sortie

y_in = -0.3 + (z₁) (0.5) + (z₂) (0.1) = 0.046

4. Out de la couche de sortie

y = 1 / (1+ exp (- y_in)) = 0.511

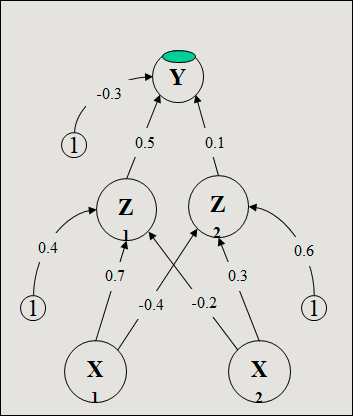
Trouver les nouveaux poids du réseau de la figure ci-dessous si on présente le vecteur d’apprentissage (0,1). a=1 et h=0,25. Avec valeur désirée t=1.

5. Erreur

t – y = 1 – 0.511 = 0.489

6. dk

dk = (t – y) (y) (1 – y) = 0.122

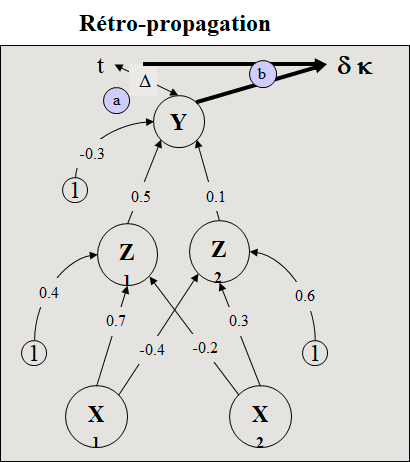
Trouver les nouveaux poids du réseau de la figure ci-dessous si on présente le vecteur d’apprentissage (0,1). a=1 et h=0,25.

Dans le cas général :

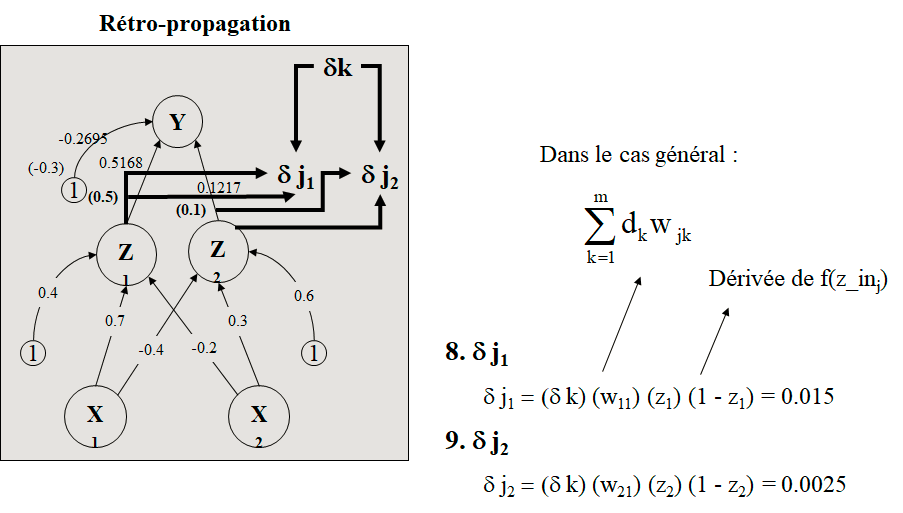
Trouver les nouveaux poids du réseau de la figure ci-dessous si on présente le vecteur d’apprentissage (0,1). a=1 et h=0,25.

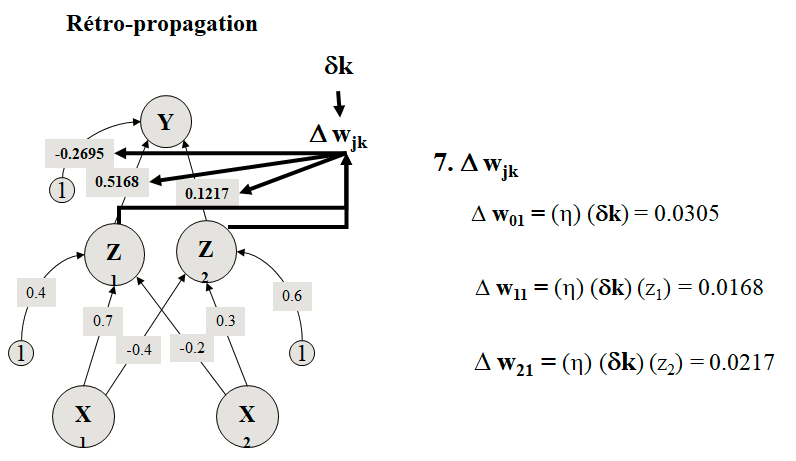
Trouver les nouveaux poids du réseau de la figure ci-dessous si on présente le vecteur d’apprentissage (0,1). a=1 et h=0,25.

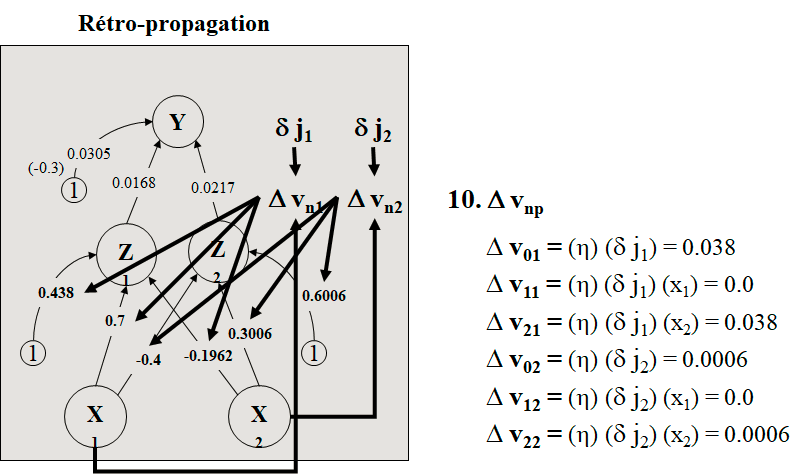
Exercice à faire:

Trouver les nouveaux poids du réseau de la figure ci-dessous si on présente le vecteur d’apprentissage (-1,1) et on utilise une sigmoïde bipolaire comme fonction d’activation

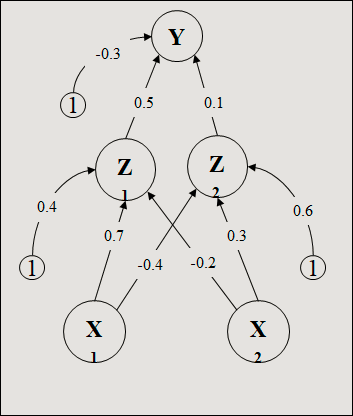
Seuls changent la dérivée de la fonction d’activation bipolaire et la mise à jour des poids entre l’entrée et la couche cachée.

Exercice2

Soit le perceptron multicouche suivant (V, W matrices poids  et d_i sortie désirée):

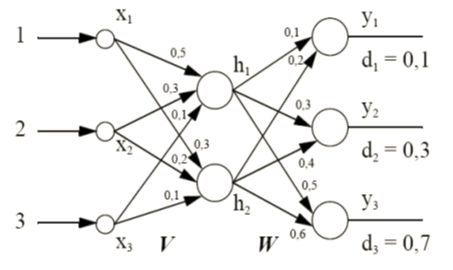
Dans l’unique but de simplifier les calculs, les neurones ne sont pas munis de l’habituel paramètre de polarisation (seuil). Les poids de connexion affichés directement sur la connexion sont résumés dans les deux matrices de connexion :

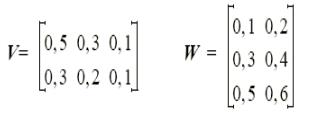
Pour le vecteur d’entrée (1,2,3)^t :

– Donner les erreurs à la sortie (calcul intermédiaire) :  d₁, d₂  et d₃

– Calculez les nouvelles valeurs de poids des V₁₁ et W₁₁  par rétropropagation du gradient.

Les paramètres du réseau sont :

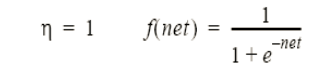
net = somme pondérée au niveau d’une cellule.

h : coefficient d’apprentissage

Solution:

Exercice 3

solution

Question ?

Quand utiliser des réseaux de neurones artificiels pour résoudre des problèmes d’apprentissage?

• lorsque les données sont représentées par des paires attribut-valeur,

• lorsque les exemples d’apprentissage sont bruités,

• lorsque des temps d’apprentissage (très) longs sont acceptables,

• lorsqu’une évaluation rapide de la fonction apprise est nécessaire,

Applications des RNA

• Contrôle

  – conduite automatique de véhicules:

  • Alvinn: réseau de pilotage d’un véhicule à partir d’images vidéo,

  – synthèse vocale:

  • NETtalk: un réseau qui apprend à prononcer un texte en anglais

  – processus de fabrication/production,

• Reconnaissance/classification/analyse

  – textes imprimés, caractères manuscrits (codes postaux), parole,

  – images fixes (ex. visages), animées ou clips vidéo,

  – risques (financiers, naturels, etc.)

• Prédiction

  – économie, finances, analyse de marchés, médecine,

  – …

Bibliographie

• Hopfield, J. J. (1982). Neural networks and physical systems with

emergent collective computational abilities. Proceedings of the National

Academy of Sciences 79:2554-2558.

• Hertz, J., A. Krogh, and R. G. Palmer. (1991). Introduction to the

Theory of Neural Computation. Redwood City, CA: Addison-Wesley.

• Rumelhart, D. E., J. McClelland, and the PDP Research Group. (1986).

Parallel Distributed Processing: Explorations in the Microstructure of

Cognition. Cambridge, MA: MIT Press.

• Bishop, C. M. (1995). Neural Networks for Pattern Recognition. New

York: Oxford University Press.

• Haykin, S. (1994). Neural Networks: A Comprehensive Foundation.

New York: Macmillan College Publishing.

• Churchland, P. S., and T. J. Sejnowski. (1992). The Computational

Brain. Cambridge, MA: MIT Press.

• Arbib, A. M. (1995). The Handbook of Brain Theory and Neural

Networks. Cambridge, MA: MIT Press.

• Sejnowski, T. (1997). Computational neuroscience. Encyclopedia of

Neuroscience. Amsterdam: Elsevier Science Publishers.

Telecharger PDF