Université Cadi Ayyad
Ecole Normale Supérieure de Marrakech
Plan
Notions de base
RdP Particuliers
Graphe de marquages
Algébre Linéaire
Introduction aux Réseaux de Petri
Les Réseaux de Petri (RdP) permettent de modéliser des systèmes séquentiels. Ils ont été inventés par Carl Adam Petri, un mathématicien Allemand contemporain (d’où l’absence d’accent dans Petri).
Il a défini un outil mathématique très général permettant de décrire les relations existant entre des conditions et des événements et de modéliser le comportement de systèmes dynamiques à événements discrets.
Ces RdP datent de 1960-1962. C’est un outil très général, modélisant aussi bien les protocoles de communication informatiques que des systèmes de production.
Le Marquage
Chaque place contient un nombre entier positif ou nul de marques ou jetons. Le marquage M définit l’état du système décrit par le réseau à un instant donné.
C’est un vecteur colonne de dimension le nombre de places dans le réseau.
Le iéme élément du vecteur correspond au nombre de jetons contenus dans la place Pi.
Exemple:
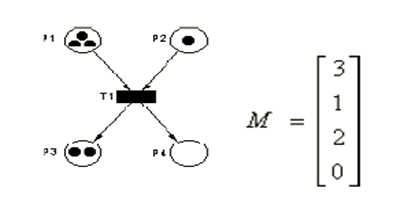
Franchissement d’une transition
Une transition est franchissable lorsque toutes les places qui lui sont en amont (ou toutes les places d’entrée de la transition) contiennent au moins un jeton.
Exemple:
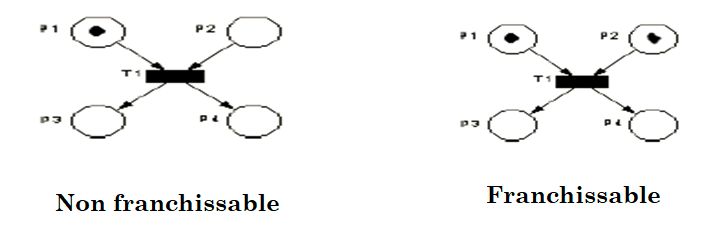
Le franchissement consiste à retirer un jeton de chacune des places d’entrée et à rajouter un jeton à chacune des places de sortie de la même transition.

Transition source:
Une transition sans place d’entrée.
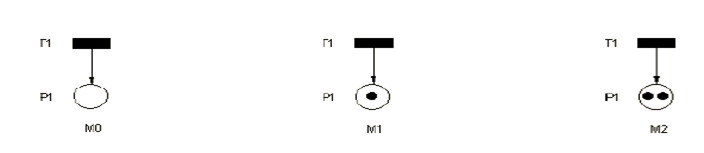
Transition puits:
Une transition sans place de sortie.
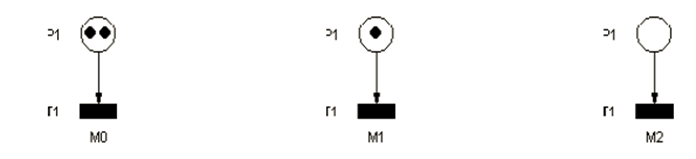
Séquence de franchissement
Une séquence de franchissement S est une suite de transitions Ti Tj…Tk qui peuvent être franchies successivement à partir d’un marquage donné. Une seule transition peut être franchie à la fois.
On note : :
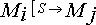
ou
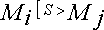
à partir du marquage Mi , le franchissement de la séquence S aboutit au marquage Mj.
Exemple:
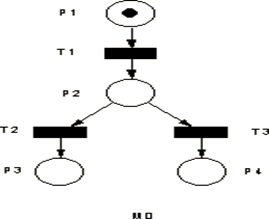
T1T2 et T1T3 sont deux séquences de franchissement:
Marquages accessibles:
L’ensemble des marquages accessibles est l’ensemble des marquages Mi qui peuvent être atteint par le franchissement d’une séquence S à partir du marquage initial M0.
On le note *M0.
Exemple:
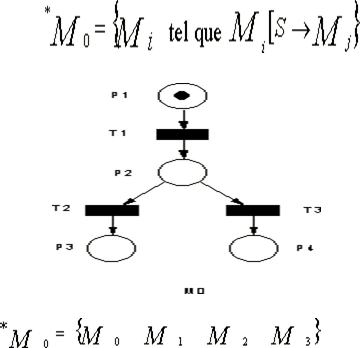
Réseaux de Petri (RdP) : autonome et non autonome
Un RdP autonome décrit le fonctionnement d’un système dont les instants de franchissement ne sont pas connus ou indiqués.
Un RdP non autonome décrit le fonctionnement d’un système dont l’évolution est conditionnée par des événements externes ou par le temps.
Un RdP non autonome est synchronisé et/ou temporisé.
Réseaux de Petri (RdP) Particuliers
1.Graphe d’état
2.Graphe d’événement
3.RdP sans conflit
4. RdP à choix libre
5.RdP simple
6.RdP pur
7.RdP généralisés
8.RdP à capacités
9.RdP à priorités
Les Réseaux de Petri (RdP) : Graphe de marquages
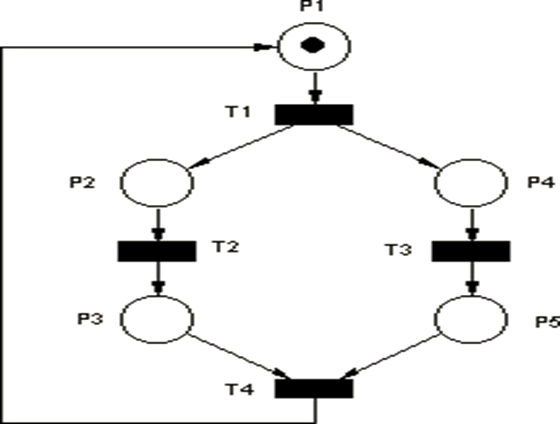
le graphe de marquages correspondant :
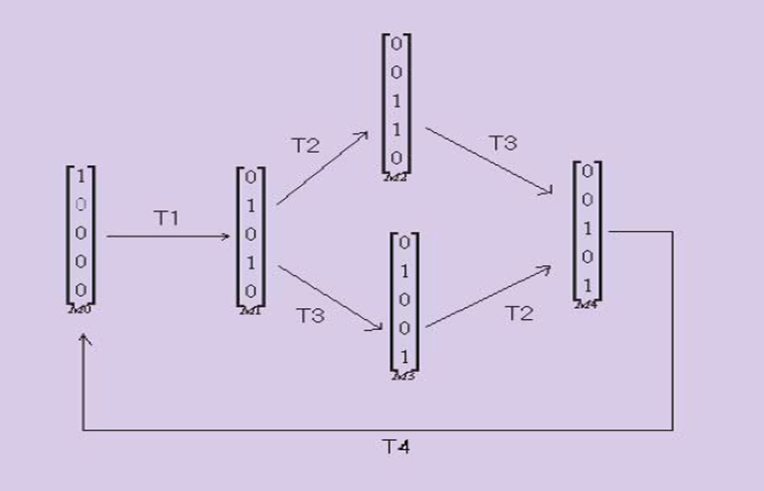
Les propriétés des Réseaux de Petri (RdP):
Une place Pi est bornée pour un marquage initial M0 si pour tout marquage accessible à partir de M0 le nombre de marques dans Pi est fini.
Un Réseau de Petri (RdP) est borné pour un marquage initial M0 si toutes les places sont bornées pour M0.
Un Réseau de Petri (RdP) est sauf pour un marquage initial M0 s’il y a une marque au plus dans chaque place, pour tout marquage accessible à partir de M0.
Un Réseau de Petri (RdP) est vivant pour un marquage initial M0 si toutes ses transitions sont vivantes.
Un blocage est un marquage tel qu’aucune transition n’est validée.
Un Réseau de Petri (RdP) est dit sans blocage pour un marquage initial M0 si aucun marquage accessible n’est un blocage.
Un Réseau de Petri (RdP) a un état d’accueil Ma pour un marquage initial M0 si pour tout marquage accessible Mi ∈*M0,
il existe Si tel que Mi →Ma.
Un Réseau de Petri (RdP) est réinitialisablepour un marquage initial M0 si M0 est un état d’accueil.
Algébre Linéaire
