Cours d'Algorithmique : Les Arbres (ABR, AVL) + Parcours infixe, préfixe et post fixe

Université Cadi Ayyad

Ecole Normale Supérieure de Marrakech

Licences professionnelles de qualification dans les métiers de l’éducation Option Informatique (S5)

Plan du Cours d’Algorithmique

Cours d’Algorithmique: Présentation général
Cours d’Algorithmique : Arbre Binaires de Recherches(ABR).
- –Définitions
- –Insertion
- –Recherche
Cours d’Algorithmique: Arbres équilibrés(AVL).
- –Définitions
- –Insertion
- –Suppression
Cours d’Algorithmique: Parcours infixe, préfixe et post fixe

Arbres

Un arbre est une structure de données organisées de façon hiérarchique, à partir d’un nœud distingué appelé racine.
Très importante en informatique!.
Arbre de jeux (i.e., Echecs ), système de fichiers UNIX/Windows, Arbres de tri etc.
Nous étudierons deux types d’arbres : Arbre Binaires de Recherches et Arbres équilibrés

Arbres: définitions

Un arbre est un ensemble de Nœuds, reliés par des Arêtes. Entre deux nœuds il existe toujours un seul chemin.

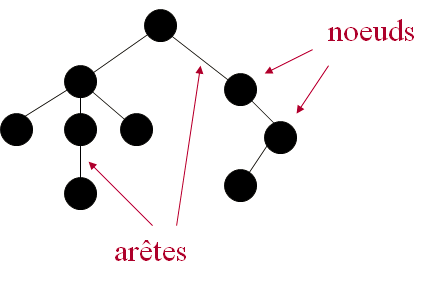
Les arbres sont enracinés. Une fois la racine définit tous les nœuds admettent un niveau.
Les arbres ont des noeuds internes et des feuilles (nœuds externes). Chaque noeud (à l’exception de la racine) a un parent et admet zéro ou plusieurs fils.

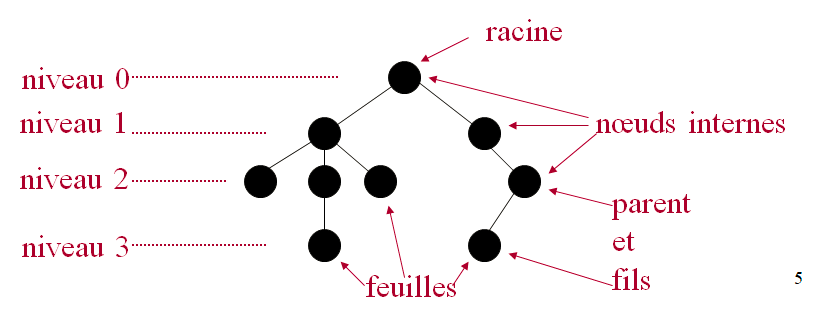
Les arbres ont des noeuds internes et des feuilles Cours d'Algorithmique

Arbres binaires

Un Arbre Binaire est un arbre où chaque nœud admet au plus 2 fils.

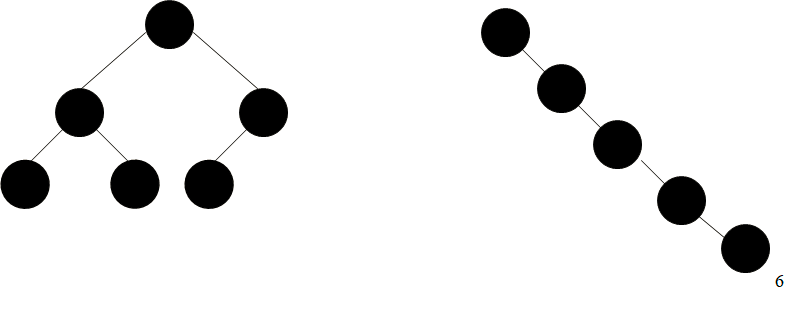
Arbres Binaires: définitions

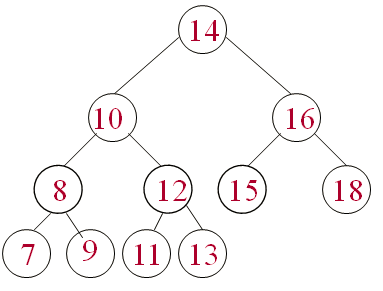
Les Nœuds d’un arbre contiennent des clés (mots, nombres, etc)
Arbre Binaire parfait : les feuilles sont toutes situées dans les deux derniers niveaux. Les feuilles du dernier niveau sont toutes à gauche.

Arbres Binaires: représentation par tableaux

Un arbre binaire complet peut être représenté par un tableau A avec un accès en O(1) à chaque noeud:
- –Mémoriser les neouds séquentiellement de la racine aux feuilles et de gauche vers la droite.
- –Fils gauche de A[i] est en A[2i]
- –Fils droit de A[i] est en A[2i + 1]
- –Parent de A[i] est en A[i/2]

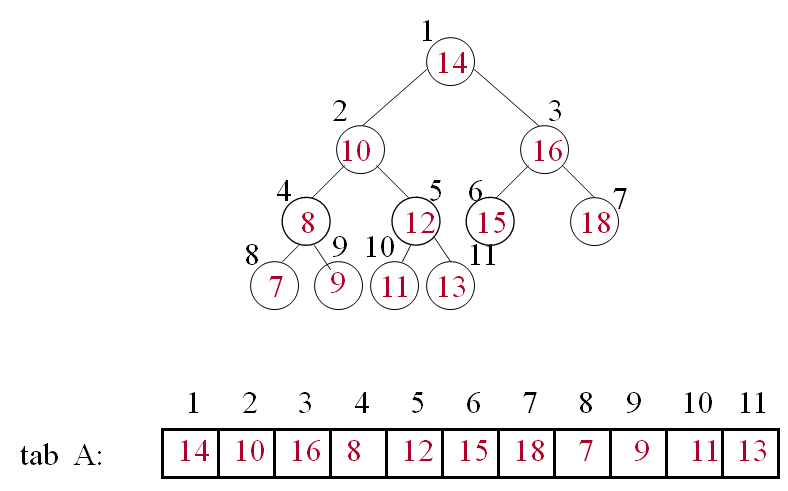
Arbres Binaires: représentation par pointeurs

typedef struct n{
  int clé;
  struct n *fGauche, *fDroit;
}nœud;

typedef nœud * Arbre;

Arbre Binaire de Recherche

Un Arbre Binaire de Recherche (ABR) est un arbre binaire avec les propriétés suivantes :
- –La clé associée à un noeud est supérieur aux clés des nœuds de son sous-arbre gauche
- –La clé associée à un noeud est inférieur aux clés des nœuds de son sous-arbre droit

Arbre Binaire de Recherche: Exemples

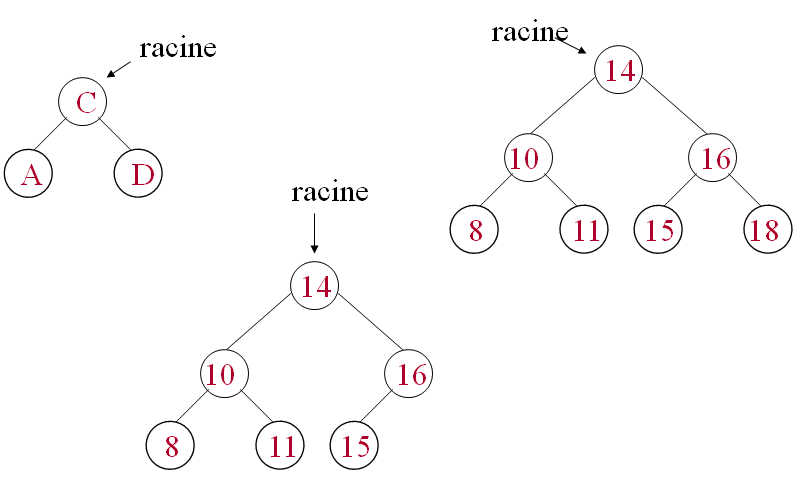
Arbre Binaire de Recherche

ABR est un arbre avec la propriété suivante :

Clé.fGauche < Clé.parent < Clé.fDroit

NOTER! Le parcours InOrdre visite les clés dans l’ordre croissant.

void inOrdre(Arbre racine) {
     inOrdre(racine->fGauche)
     print(racine->key)
     inOrdre(racine->fDroit)
}

ABR : Rechercher un élément

Soit un ABR :

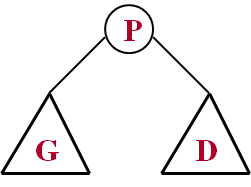
Problème: rechercher un noeud avec une clé x ?

rechercher(racine, x)
  comparer x à la clé de racine:

     - si x = clé return
     - si  x < clé => chercher dans G
     - si  x > clé => chercher dans D

    chercher de la même manière dans G ou D

Exemple:

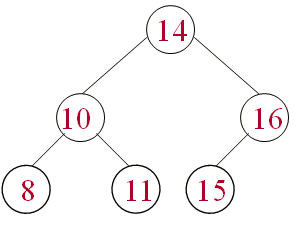
x=8 (oui) x=17 (non)

bool searchABR(Arbre racine; typeCle clé){
  if (racine==NULL)  return false
  if (racine->clé==clé)
  return true;
  else if (key < racine->clé)
      return searchABR(racine->fGauche, clé);
  else
      return searchABR(racine->fDroit, clé)
}

Donner une version itérative ?

ABR : Ajout d’un élément

Comment ajouter une clé?

La même procédure que searchABR s’applique: Déterminer la position d’insertion par searchABR. Ajouter la nouvelle clé si la recherche échoue.

Exemple:

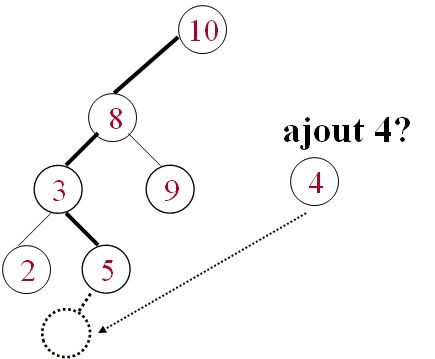
cours algorithmique ABR : Ajout d’un élément. ajouter un element

Construction d’un ABR

Exemple: ajouter C A B L M (dans l’ordre!)

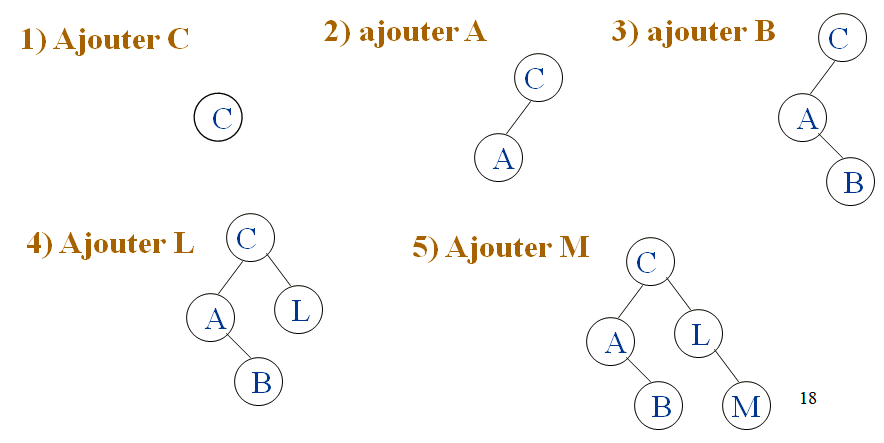
L’ABR est-il unique pour une séquence de lettres A B C L M ?

NON! différentes séquences donnent différents ABR

Trier avec un ABR

Soit un ABR, peut-on afficher les clés dans l’ordre?

Visiter l’ABR avec un parcours InOrdre:

– visiter le sous-arbre gauche

– afficher racine

– visiter le sous-arbre droit

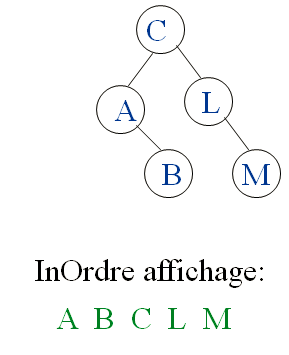
Comment trouver le minimum?

Comment trouver le maximum?

ABR : supprimer un élément

Pour supprimer un nœud contenant x, rechercher x, une fois trouvé appliquer l’un des trois cas suivants:

CAS A: x est une feuille

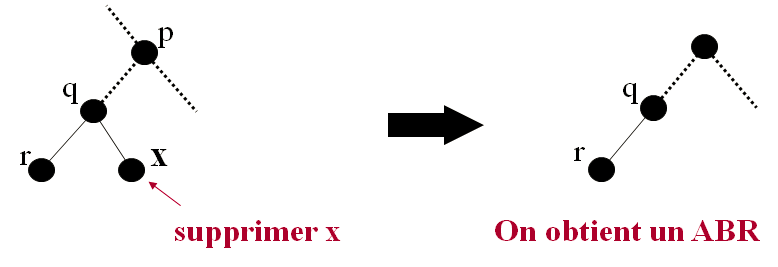
Cas B: x est un nœud interne avec un seul sous-arbre

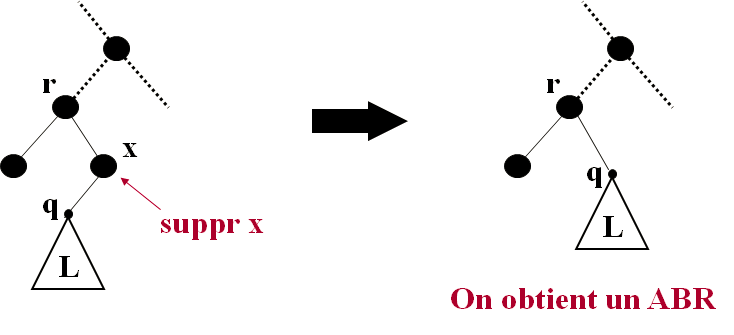
Cas C: x est un nœud interne avec 2 sous-arbres

x est un nœud interne avec 2 sous-arbres cours algo abr

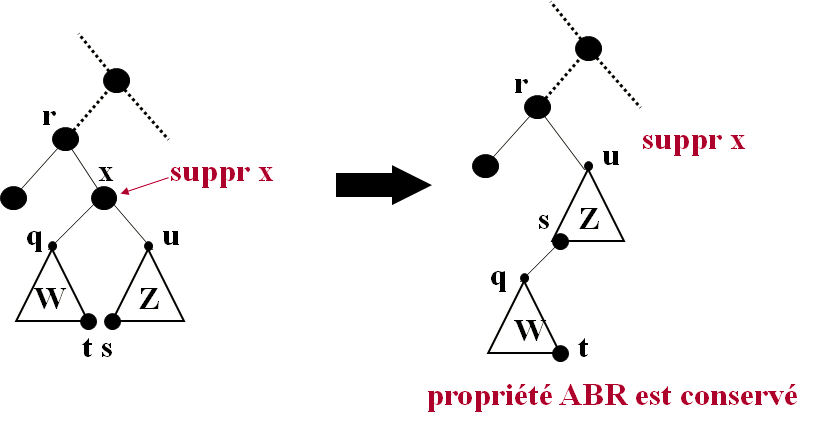
Cas C suite: … ou encore comme suit

q  <  x  <  u

=>  q est inférieur au plus petit
     élément de Z
=>  r est supérieur au plus grand
      élément de W

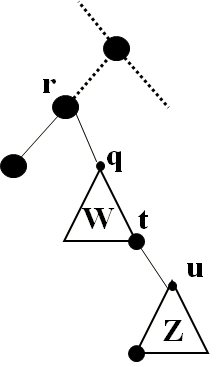
D’autres façon ?

ABR : Compléxité de rechercher

•il est nécessaire d’avoir un ABR plein ou niveau-min ABR

=> garder un arbre le plus équilibré possible à tout moment (Arbre AVL)

Arbre AVL

Arbre AVL (Adelson-Velskii et Landis):
- Le meilleur ABR maintenant à tout moment un arbre raisonnablement équilibré.
- Idée : si l’insertion ou la suppression provoque un désiquilibre de l’arbre, rétablir l’équilibre.
- Toutes les opérations insertion, suppression,… sur un arbre AVL avec N noeuds en O(log N) (en moyenne et dans le pire cas!)

AVL Trees

Arbre AVL (propriété): c’est un ABR tq. la différence des hauteurs du sous-arbre gauche et droit de la racine est au max 1 et les sous-arbres gauche et droit sont des AVL

Exemple:

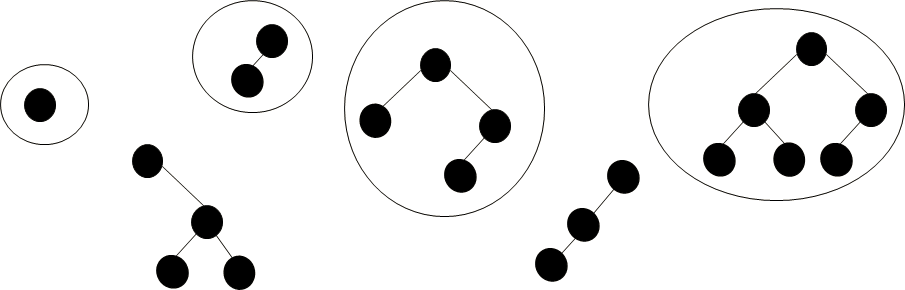
Arbres AVL

Pour plus lisibilité , remplaçer les clés associées aux nœuds en utilisant /, \, -, // et \\ pour représenter le facteur d’équilibre d’un nœud :

/ : léger déséquilibre à gauche
\ : léger déséquilibre à droite
– : équilibré
\\ : déséquilibre droit
// : déséquilibre gauche

h(G) = 1 + h(D)
h(D) = 1 + h(G)
h(D) = h(G)
h(D) > 1 + h(G)
h(G) > 1 + h(D)

Exemples :

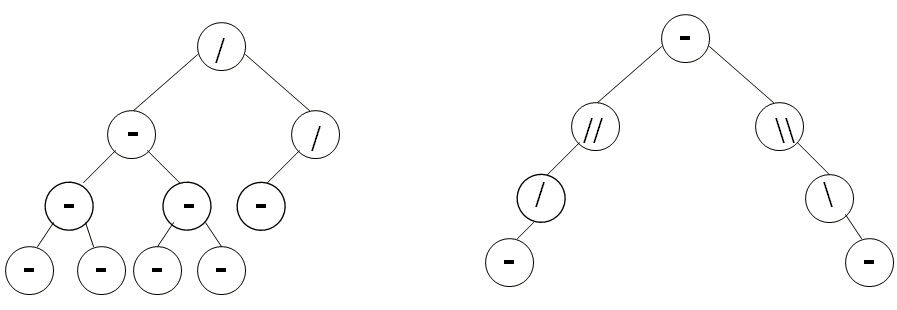
Les clés ne sont pas montré.

On suppose qu’elles satisfassent la propriété ABR

Un arbre AVL n’est ni un arbre plein ni un arbre niveau-min.

Insertions et suppression sont éffectuées de la même manière que pour les ABR. Après chaque opération, on a besion de vérifier la propriété d’AVL!. Car l’arbre peut ne plus l’être!

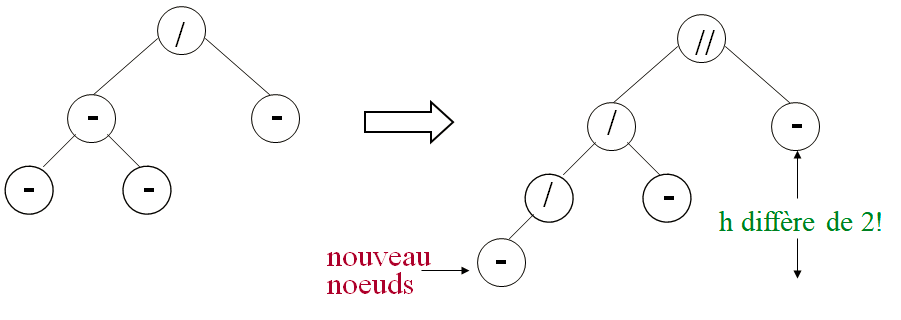
Après une insertion, si l’arbre est un AVL alors on ne fait rien.

Comme sur l’exemple ci-dessous :

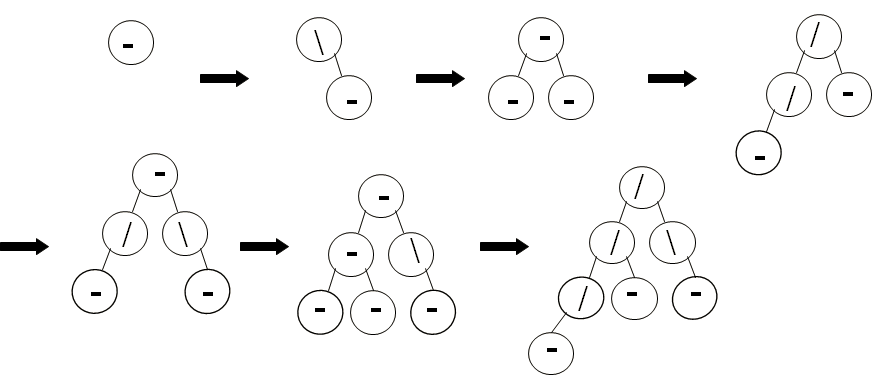
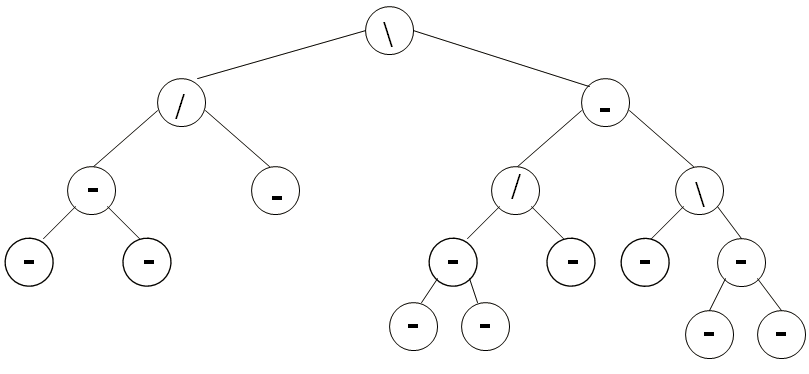
Quand une insertion provoque le déséquilibre de l’arbre?

Arbres AVL : insertion d’un noeud

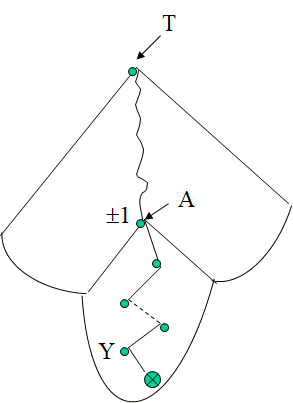
L’arbre devient déséquilibré si l’élément ajouté est le descendant gauche (droit) d’un nœud avec un léger déséquilibre gauche (droit). Alors la hauteur de ce sous-arbre augmente.

Dans les figure suivantes, on note :

U: nouveaux nœuds pouvant déséquilibrer l’arbre

B: nouveaux laissant l’arbre équilibré

Arbres AVL: Insertion

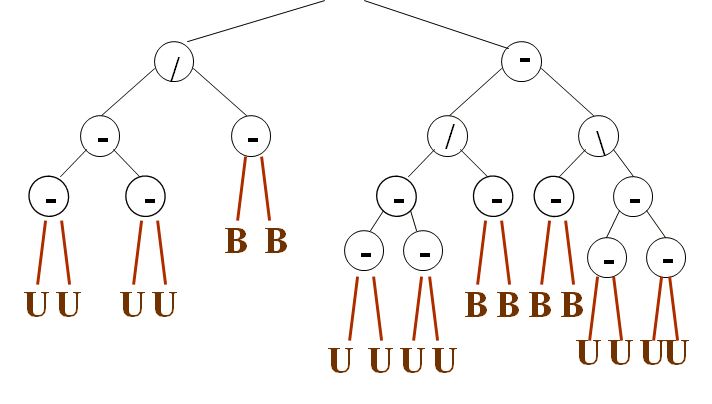
Noter que l’insertion d’un nœud peut provoquer des déséquilibre sur plusieurs nœuds.

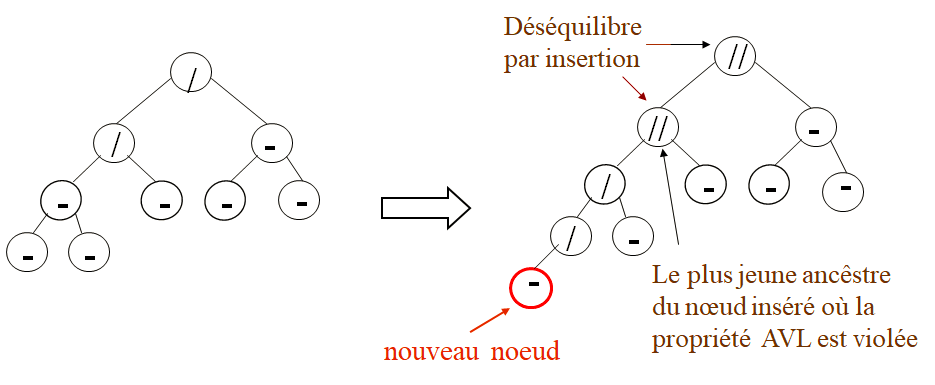
Supposons que le sous-arbre le plus haut est celui de gauche et qu’un nœud est inséré pour augmenter la hauteur de ce sous-arbre. L’arbre obtenu est déséquilibré Rétablir un arbre AVL en utilisant des rotations

=> Soit A le plus jeune ancêtre où apparaît le déséquilibre

Dans l’arbre AVL, avant l’insertion, T₁, T₂ et T₃ ont une hauteur h

Dans l’arbre AVL, avant
l’insertion, T1, T2 et T3
ont une hauteur h

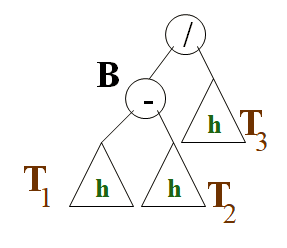
Le même raisonnement peut être utilisé si l ’arbre le plus haut est celui de droite

Cas I: un nouveau nœud est inséré dans T₁

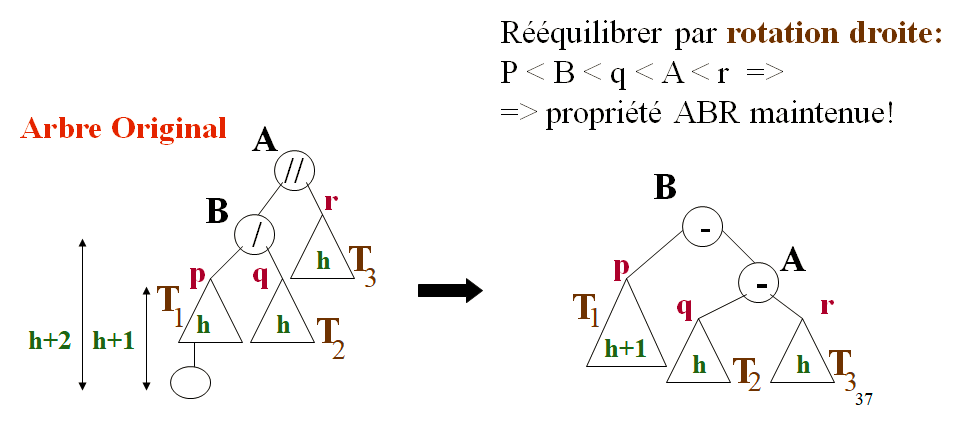
Cas I: rotation Droiteou rotation Gauche

void RD(Arbre *a){
   Arbre aux= (*a)->fg;
   (*a)->fg = aux->fd;
   aux->fd= *a;
   *a= aux;
}

void RG(Arbre *a){
   Arbre aux= (*a)->fd;
   (*a)->fd = aux->fg;
   aux->fg= *a;
   *a= aux;
}

Cas II: nouveau noeud inséré dans T₂

cours algo Cas II: nouveau noeud inséré dans T2

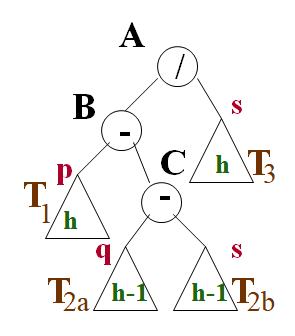
On a 3 cas a considérer :

1- nouveau nœud en C

2- nouveau nœud ajouté à T_2a

3- nouveau nœud ajouté à T_2b

Les 3 cas sont similaires.

On considérera le cas 2.

Cas II – T2a :

Rééquilibrage de l’arbre AVL avec une double rotation (gauche sur B et ensuite droite sur A)

Cas II – T2b :

Insertion en T2b => rotation droite sur B et ensuite gauche sur A

Cas II – T2a :

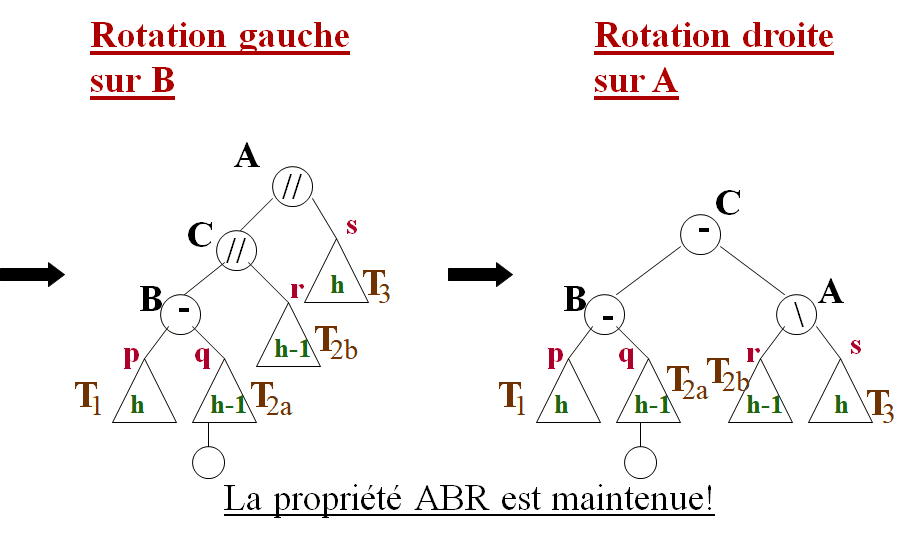
Rotation gauche
Rotation droite
Arbres AVL: Insertion cours algorithmique

Cas II: nouveau noeudinsérédans T₂

Cas II – T2a :

void RGD(Arbre *a){
   RG( &((*a)->fg) );
   RD(a);
}

Cas II – T2b :

void RDG(Arbre *a){
   RD( &((*a)->fd) );
   RG(a);
}

Nous avons défini un arbre “équilibré” et nous avons aussi montré comment insérer dans l’arbre en utilisant les algorithmes ABR de manière à maintenir l’équilibre (propriétés AVL) et la propriété ABR.

Arbre AVL: Insertion (Algorithme)

Propriété : Toute adjonction dans un AVL nécessite au plus une rotation pour le rééquilibrer.

Arbre AVL: suppression

La réorganisation de l ’arbre peut nécessiter plusieurs rotations successives.
Suppression de 26 et de le remplacer par 24

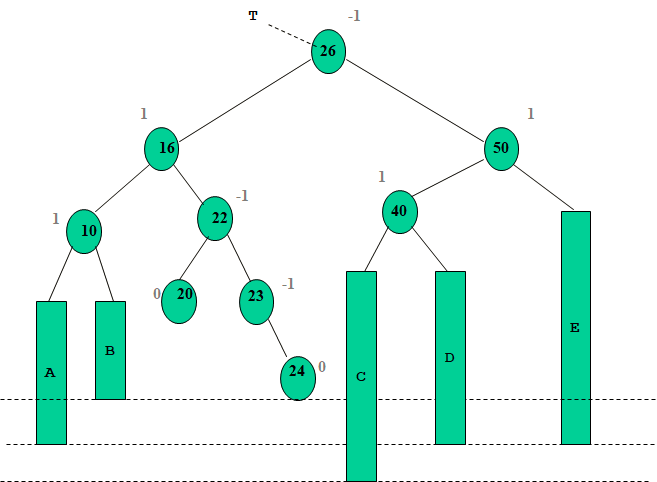
L ’arbre n ’est plus un AVL

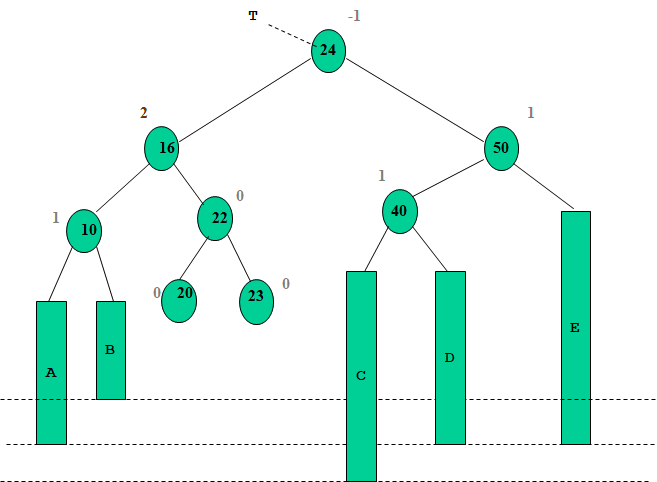
L ’arbre n ’est plus un AVL

Arbre AVL: suppression
algorithmique

On distingue différents cas…

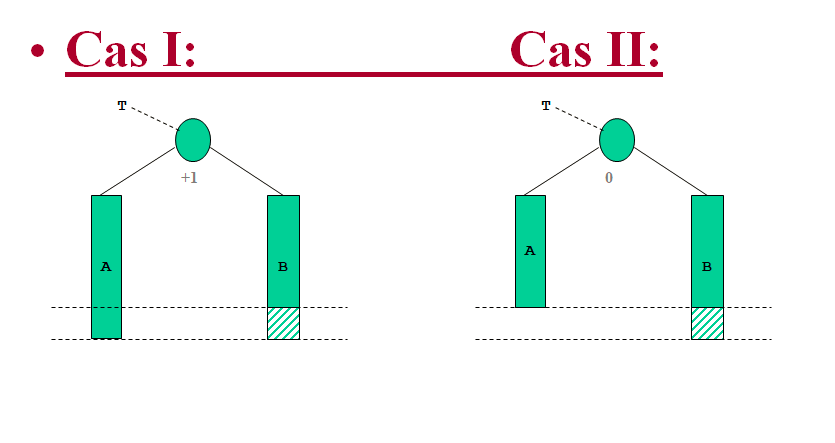
• Rien à faire, car la hauteur de l’arbre n’a pas été modifié
• Avec -1 même situation

• Ici la hauteur du sous-arbre va évoluer(-1) localement :
aucun déséquilibre n ’est apparu, au contraire, le sous arbre devient équilibré.
Des déséquilibre peuvent apparaître plus haut!

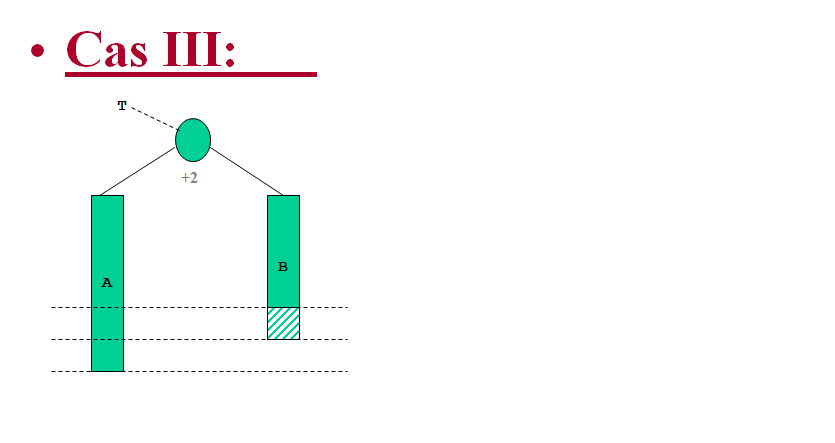
Ici la hauteur du sous-arbre n’a pas évolué mais le déséquilibre est passé à 2 : il faut intervenir; on distingue la différents cas de figure qui sont liées au fils gauche :

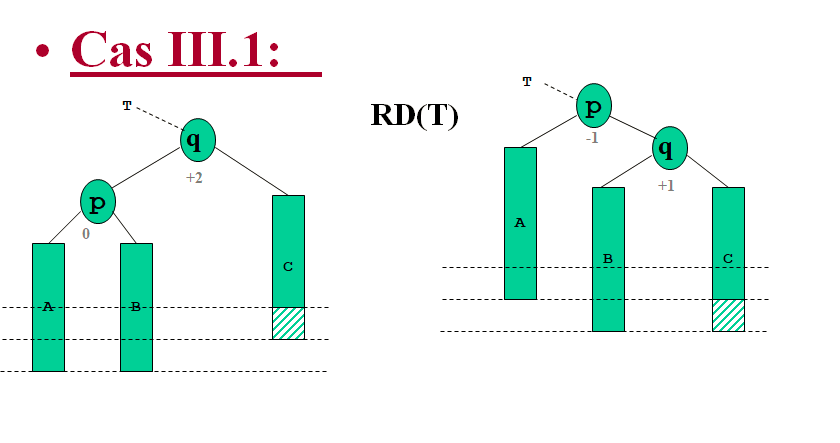
Il y a arrêt du traitement ici, puisque :

le sous-arbre est équilibré
sa hauteur n’a pas été modifiée (il est donc inutile de propager le résultat vers le haut)

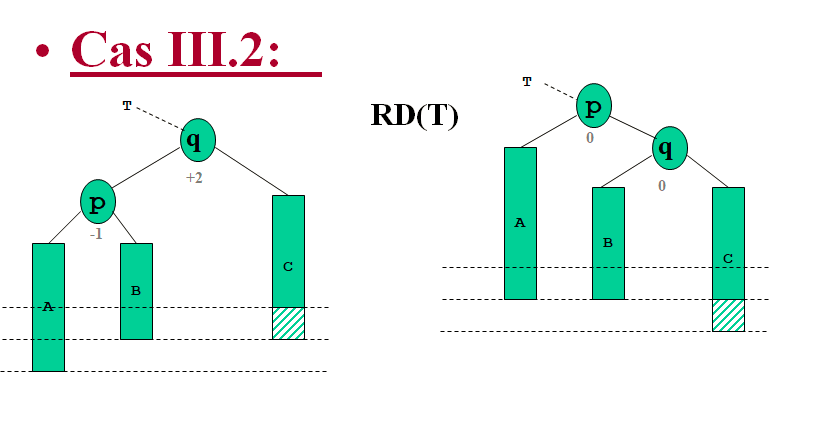
Le sous-arbre est rééquilibré, mais la hauteur a été modifié ,il faut remonter l ’information au dessus de T pour procéder éventuellement à des rééquilibrage

=> appliquer le même principe que celui qui vient d ’être appliqué en considérant I,II et les différents cas de III.

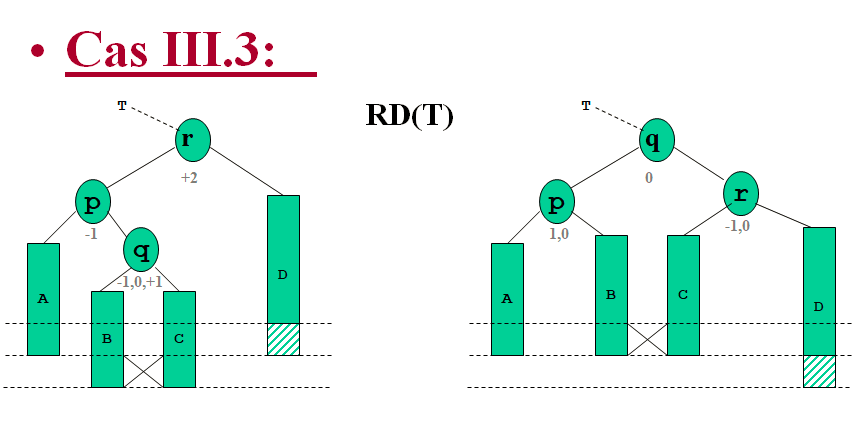
Le sous-arbre est rééquilibré, mais sa hauteur a diminué de 1

=> remonté de l ’information comme en III.2

Cours d’Algorithmique : Principe de l ’algorithme :

– Réorganisation de l ’arbre de la feuille supprimée jusqu ’à la racine de l ’arbre avec éventuellement des rotations (on s’arrête pour les cas I ou III.1)

recalcul des déséquilibres occasionnés par la suppression et éventuelle exécutions des rotations nécessaires du fait de nouveaux déséquilibres
la propagation continue tant que l ’arbre demeure déséquilibré lors de la remontée

Au pire cas le nombre de rotation est log₂ n

Parcours d’arbres

Parcourir un arbre signifie visiter dans un certain ordre tous ses nœuds. Les parcours les plus classiques sont les parcours

infixé,
préfixé
postfixé.

Ces parcours sont définis récursivement de la manière suivante :

Infixe (symétrique) : on parcourt d’abord le premier sous-arbre en infixé, puis la racine, puis chacun des autres sous-arbres, en infixe.

Voici, l’ordre de visite des nœuds pour le parcourt infixe :

L J E B F A C G D H K I

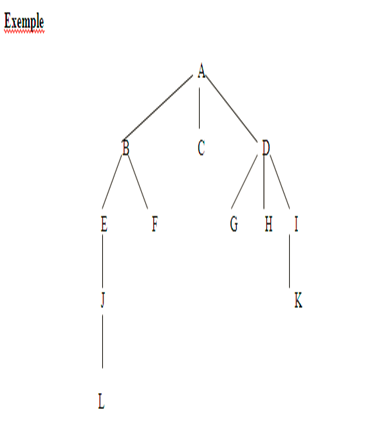
l’ordre de visite des nœuds pour le parcourt infixe

Préfixe : on parcourt d’abord la racine, puis chacun des sous-arbres en préfixe.

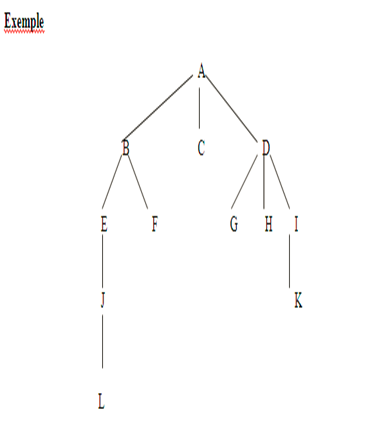
l’ordre de visite des nœuds pour le parcourt préfixe

Voici, l’ordre de visite des nœuds pour le parcourt préfixe :

A B E J L F C D G H I K

Postfixe : on parcourt d’abord tous les sous-arbres en postfixe, puis on parcourt la racine.

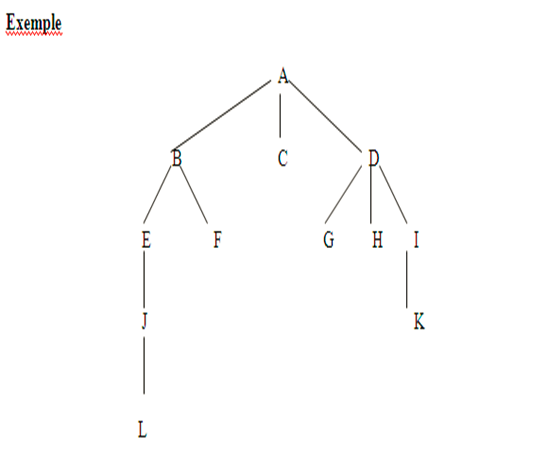
l’ordre de visite des nœuds pour le parcourt postfixe

Voici, l’ordre de visite des nœuds pour le parcourt postfixe :

L J E F B C G H K I D A

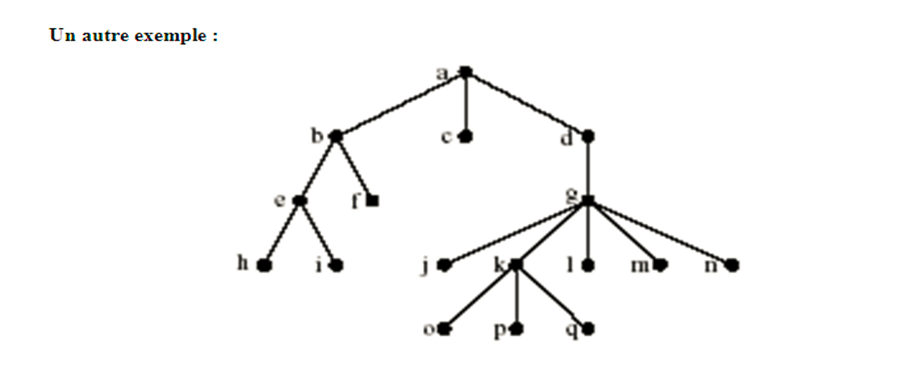
Infixe : h e i b f a c d j g o k p q l m n

Prefixe : a b e h i f c d g j k o p q l m n

Postfixe : h i e f b c j o p q k l m n g d a

Telecharger PDF