Plan de la séquence
- Introduction
- Définitions
- La complexité d’un algorithme asymptotique
- Notation grand O
- Définition
- Exemple
- Règles de simplification
- règles pour calculer la complexité d’un algorithme
- Les classes de calcule
- Un Exemple réel (tri)
- Algorithme Rapide VS Algorithme lent
Problème !
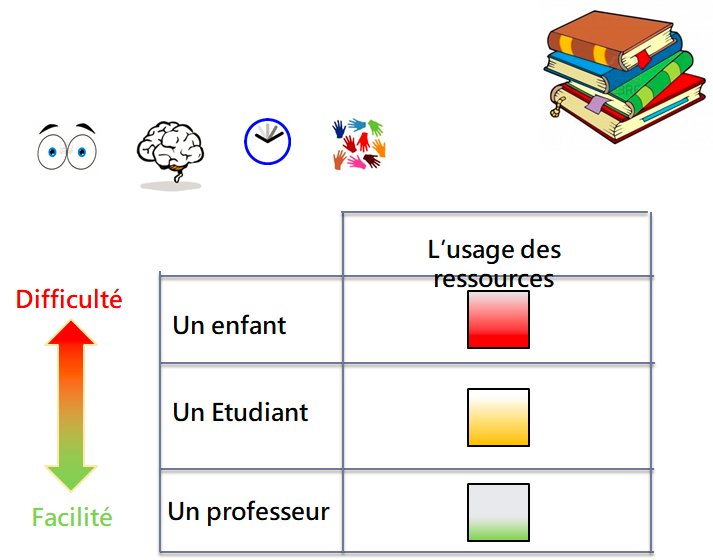
Nous avons : Un enfant, un étudiant, un professeur
Leurs Objectif : trouver un mot dans un dictionnaire !
Leurs ressources
Introduction
- C’est quoi un algorithme ?
- Une succession d’instructions qui renvoie un résultat, afin de résoudre un problème.
- Quel est l’environnement d’un algorithme ?
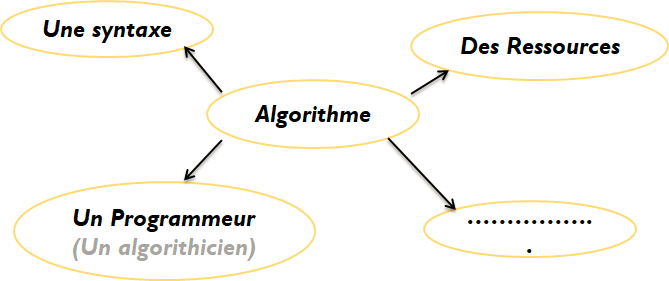
- Comment juger un algorithmes ? Quel critères ?
- Usage des ressources
- En informatique (Mémoire, CPU, Temps )
- Usage des ressources
- C’est quoi une complexité d’un algorithme?
- La complexité = une mesure (exemple : mètre, Litre, hectare, …)
- Pour comparer les algorithmes
- Pour dire quelle algorithme est la moins complexe
- Pour dire que cette algorithmes est la plus efficace
- Pour dire quelle algorithme est la moins complexe
- Pour comparer les algorithmes
- La complexité = une mesure (exemple : mètre, Litre, hectare, …)
Definitions
- C’est quoi l’analyse de la complexité d’un algorithme?
- Etudier formellement la quantité de ressources en temps (complexité temporelle) et en espace (complexité spatiale) nécessaires pour l’exécution d’un algorithme donnée.
- Le nombre d’opérations élémentaires (affectation, comparaison, …) affectées par un algorithme. (retenez « n »)
- C’est quoi la l’efficacité d’un algorithme ?
- C’est l’usage du minimum des ressources
- Le Meilleur algorithme = le plus efficace = le moins complexe l
- C’est l’usage du minimum des ressources
- Comment évaluer l’efficacité d’un algorithme ?
- Approche dépendante des facteurs matériaux
- Approche indépendante des facteurs matériaux
La complexité d’un algorithme asymptotique
- La complexité exacte d’un algorithme est plus difficile à déterminer. On ne s’intéresse qu’à la complexité d’un algorithme dite asymptotique.
- La complexité d’un algorithme asymptotique d’un algorithme décrit le comportement de celui-ci quand la taille n des données du problème traité devient de plus en plus grande, plutôt qu’une mesure exacte du temps d’exécution.
- Une notation mathématique, permettant de représenter cette complexité d’un algorithme asymptotique c’est la notation grand O.
Notation grand O

−Signification: Pour toutes les grandes entrées (i.e., n >= n0), on est assuré que l’algorithme ne prend pas plus de Cg(n) étapes.
−Exemple
f(n) = 3n2 +2n + 1. => On a : f(n) = O(g(n)).
g(n) = n2.
Grand-O: Exemple
Exemple 1: Initialiser un tableau d’entiers
for (int i=0; i<n; i++) Tab[i]=0;
Supposons que chaque itération nécessite un temps <= c,
où c est une constante (accès au tableau + une affectation).
Il y a n itérations
Le temps est donc T(n) <= cn
Donc T(n) = O(n)
Grand-O: Règles de simplification
- Si f(n) = O(g(n)) et g(n) = O(h(n)),
alors f(n) = O(h(n)).
- Si f(n) = O(kg(n)) où k > 0 est une constante,
alors f(n) =O(g(n)).
- Si f1(n) = O(g1(n)) et f2(n) = O(g2(n)),
alors (f1 + f2)(n) = O(max(g1(n), g2(n))).
- Si f1(n) = O(g1(n)) et f2(n) = O(g2(n)), alors f1(n)f2(n) = O(g1(n) g2(n)).
Règles pour calculer la complexité d’un algorithme
- Règle 1: Les opérations élémentaires telle que l’affectation, test, accès à un tableau, opérations logiques et arithmétiques, lecture ou écriture d’une variable simple … etc, sont en O(1).
- Règle 2: Instruction if:
maximum entre le then et le else.
Règle 3: Instructions de répétition: la complexité de la boucle for est calculée par la complexité du corps de cette boucle multipliée par le nombre de fois qu’elle est répétée.
Règles de calcule : Exemples
Exemple 1: a = b; => Temps constant: O(1).
Exemple 2:
somme = 0;
for (i=1; i<=n; i++) => Temps: O(n)
somme += n;
Exemple 3:
somme = 0;
for (j=1; j<=n; j++)
for (i=1; i<=n; i++)
somme++; => Temps: O(1) + O(n²) + O(n) = O(n²)
for (k=0; k<n; k++)
A[k] = k;
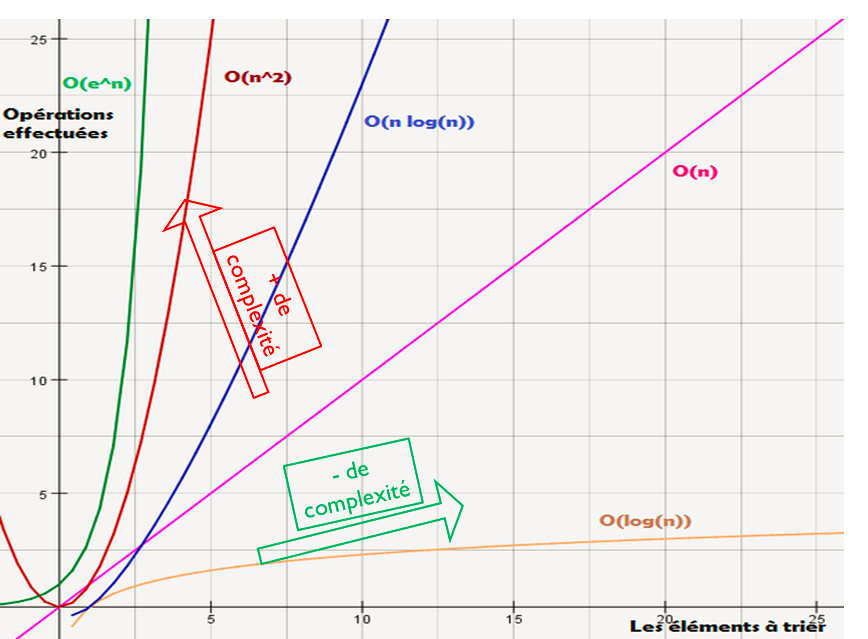
Les principals classes de complexité

Exemple de classe de complexité d’un algorithme
Complexité : O(1) - (Exemple fonction de permutation) Fonction permutation (S, i, j) var ← tab[i] ; coût C1 =1 tab[i] ← tab[j] ; coût C2 = 1 tab[j] ← var ; coût C3 = 1 Retourner S Complexité : T(n)=C1+C2+C3 T(n)=1+1+1=O(1)
complexité : O(n) - (Exemple fonction de Recherche)
Fonction Rechercher(x, S, n)
I <-- 1 ; C coût c1=1
Tant que ((I<=n) et (S[I] = ! x)) faire
{
I=I+1 ; coût c2=1
}
Retourner S ; coût c3 =1
Complexité :
T(n)=C1+ ∑1_(i=1)^n▒〖C2+C3〗
T(n)=1+ ∑1_(i=1)^n▒〖1+1)〗
T(n)=1+n+1=O(n)
complexité : O(n2) - (Exemple fonction de tri) Fonction tri (S, n) Pour i=n à 2 faire (n-1 fois) Pour j=1 à i-1 faire (i-1 fois) Si(S[j] > S[j+1]) alors Permuter S[j] et S[j+1] dans S C_perm (Cout de permutation) Complexité : T(n)=C_perm∗ ∑1_(i=0)^(n-1)▒i =C_(perm )∗(n∗(n-1))/2 =C_(perm )∗(n^2-n)/2 =C_(perm )∗n^2/2 -C_(perm )∗n/2 =C_(perm )∗n^2/2 -C_(perm )∗n/2 =O(n^2)
Rappel : ∑1_(i=0)^(n-1)▒〖i =(n∗(n-1))/2=O(n^2)〗
/* Exemple */
Un algorithme VS Un algorithme
Tri par fusion VS Tri par sélection
Tri par fusion (rappel)
Objectif:
trier les valeurs d’un tableau
Principe de l’algorithme :
« diviser pour régner »
Démarche:
1.diviser (virtuellement) le tableau de départ en deux sous-tableaux, et ainsi de suite, jusqu’à n’avoir qu’un seul élément.
2.fusionne chaque deux éléments en un tableau trié
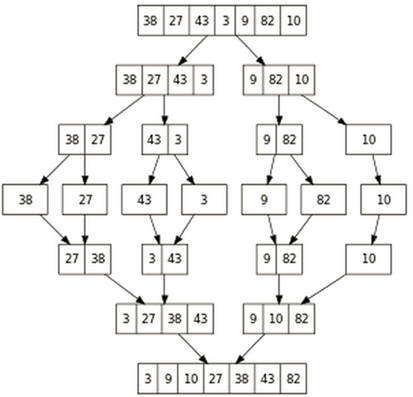
L’algorithme de tri par fusion

Rappels – règles
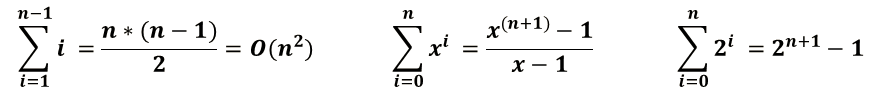
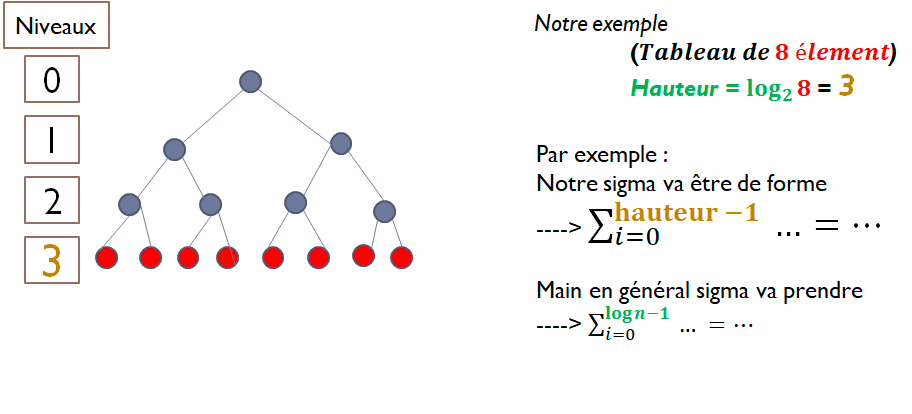
Démonstration

Tri par sélection (rappel)
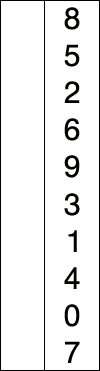
Sur un tableau de n éléments (numérotés de 1 à n), le principe du tri par sélection est le suivant :
- rechercher le plus petit élément du tableau, et l’échanger avec l’élément d’indice 1 ;
- rechercher le second plus petit élément du tableau, et l’échanger avec l’élément d’indice 2 ;
- continuer de cette façon jusqu’à ce que le tableau soit entièrement trié.
L’algorithme de tri par sélection
PRODECURE Tri_Selection (Tableau a[1:n]) VARIABLE indice_max : ENTIER; POUR i VARIANT DE 1 A n-1 FAIRE indice_max <- i; POUR j VARIANT DE i+1 A N FAIRE SI a[j]<max ALORS indice_max <- j; FIN POUR echanger a[i] et a[indice_max]; FIN POUR FIN PROCEDURE