Sciences Indusrielles
Systèmes linéaires continus invariants
ANALYSE FREQUENTIELLE
SYSTEMES LINEAIRES CONTINUS INVARIANTS
ANALYSE FREQUENTIELLE (Partie 1 & 2)
L’étude détaillée se limite aux systèmes de bases, c’est à dire aux systèmes du premier ordre et du second ordre. En effet l’étude des autres systèmes se construit à partir des résultats issus des premiers et seconds ordres.
1 Généralités – Rappels
1.1 Fonctions de transfert
Considérons le schéma bloc d’un asservissement :
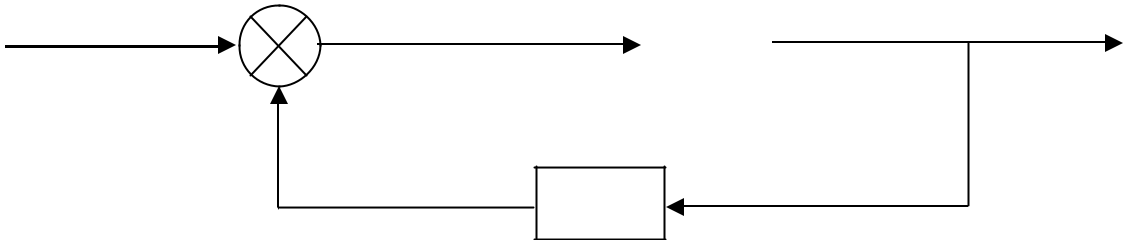
Définition des fonctions sur le schéma bloc usuel :
E ( p) est l’entrée du système ou encore la consigne donnée au système.
S ( p) est la sortie du système ou encore la réponse système.
S ¢( p) est l’image de la sortie.
- ( p) est l’erreur (ou écart) constatée entre l’entrée E ( p) et l’image de la sortie S ¢( p) .
Définition de la FTBF et de la FTBO :
- Fonction de Transfert en Boucle Fermée (abrégé sous la forme FTBF) :
S ( p)
E( p)
- Fonction de Transfert en Boucle Ouverte (abrégé sous la forme FTBO) :
FTBO = S¢( p)
- ( p)
Calcul de la FTBF et de la FTBO dans le cas de la boucle d’asservissement classique représentée ci-dessus :
FTBO = S¢( p) = A( p)B( p)
- ( p)
Page 1 Emmanuel FARGES Ó EduKlub S.A.
Tous droits de l’auteur des œuvres réservés. Sauf autorisation, la reproduction ainsi que toute utilisation des œuvres autre que la consultation individuelle et privée sont interdites.
Systèmes linéaires continus invariants
ANALYSE FREQUENTIELLE
S( p) = A( p )e ( p)
- A( p)[E( p) – S ¢( p)]
- A( p)[E( p) – B ( p) S( p)]
|
[ |
+ A( p) B( p) |
] |
= A ( p ) E( p) |
|||||||
|
S( p) 1 |
||||||||||
|
Soit la fonction de transfert en boucle fermée : FTBF = H ( p) = |
S ( p) |
|||||||||
|
H ( p) = |
A ( p) |
|||||||||
|
E ( p) |
1+ A ( p ) B( p) |
|||||||||
A ( p)
Ce qui peut encore se présenter sous la forme : FTBF = H ( p) =
1+ FTBO
Chaque fonction de transfert étant un rapport polynomial, peut donc s’écrire :
K
H ( p) = pa
|
m æ |
p |
ö |
ìa :classedusystème |
||||||||
|
ï |
|||||||||||
|
Õ |
ç1- |
÷ |
|||||||||
|
ïK :gainstatiquedusystème |
|||||||||||
|
z |
|||||||||||
|
ç |
÷ |
ïn :ordredusystème |
|||||||||
|
i =1è |
i |
ø |
où : |
||||||||
|
í |
|||||||||||
|
n |
æ |
ö |
|||||||||
|
p |
ï p |
j |
:(zérosdudénominateur)polesdelafonctiondetransfert |
||||||||
|
Õ |
ç 1- |
÷ |
ï |
||||||||
|
ç |
p |
÷ |
ï z :(zérosdunumérateur)zérosdelafonctiondetransfert |
||||||||
|
j = 1è |
j ø |
î i |
|||||||||
1.3 Analyse fréquentielle
1.3.1 Réponse harmonique
On étudie la réponse du système soumis à une entrée harmonique, c’est à dire sinusoïdale :
e(t) = E 0 sin (w t ) .
On démontre qu’une des caractéristiques des systèmes linéaires continus invariants est qu’ils présentent une réponse en régime établi (solution particulière de l’équation différentielle) de la même forme que l’entrée, c’est à dire sinusoïdale mais déphasée et d’amplitude
différente : s(t) = S0 sin (w t + j)
Page 2 Emmanuel FARGES Ó EduKlub S.A.
Tous droits de l’auteur des œuvres réservés. Sauf autorisation, la reproduction ainsi que toute utilisation des œuvres autre que la consultation individuelle et privée sont interdites.
Sciences Indusrielles
Systèmes linéaires continus invariants
ANALYSE FREQUENTIELLE
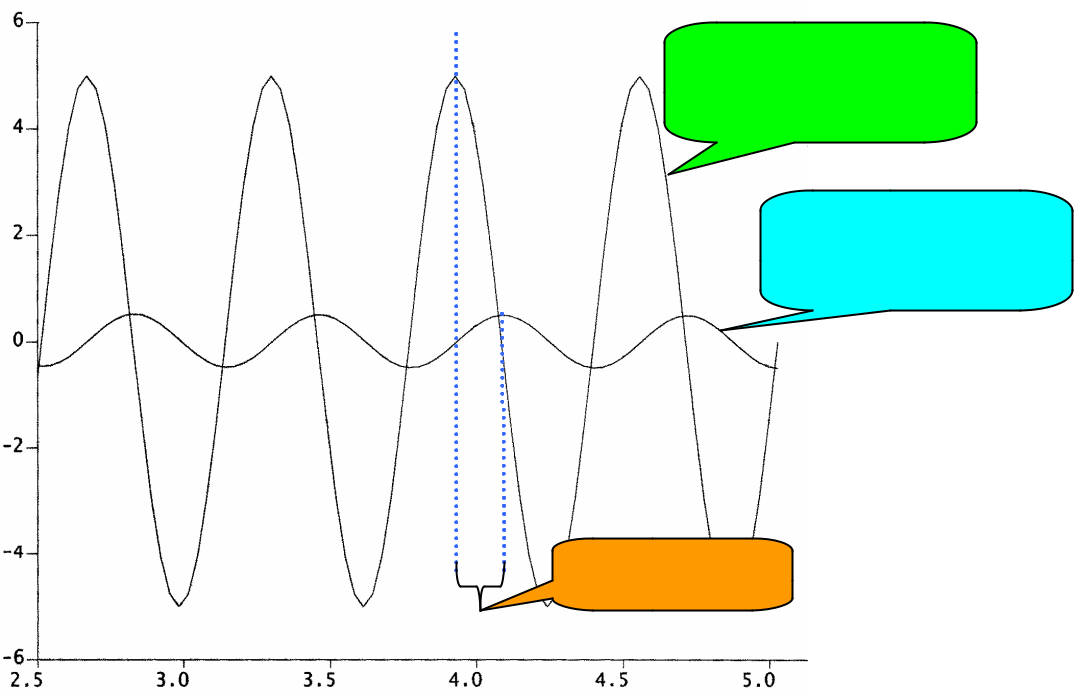
Signal d’entrée :
E0 
e(t) = E 0 sin (w t )
Signal de sortie :
s (t) = S 0 sin (w t +j )
S0 
Déphasage j
On étudie alors le rapport d’amplitude sortie sur entrée S0 et le déphasage j en fonction de E0
la pulsation du signal d’entrée w .
On montre que le rapport des amplitudes est égal au module de la fonction de transfert avec p = jw et que le déphasage est égal à l’argument de la fonction de transfert avec p = jw .
Conclusion : L’étude fréque ntielle d’un système de fonction de transfert H ( p) consiste donc à éffectuer p = jw dans l’expression de la fonction de transfert et à étudier le complexe H ( jw) souvent par son module (alors exprimé en décibels :

 H ( jw )
H ( jw ) 
 dB = 20Log
dB = 20Log 
 H ( jw)
H ( jw) 
 ) et son argument ( j (w ) = Arg [ H ( jw)]) ou bien par sa partie réelle et sa partie imaginaire.
) et son argument ( j (w ) = Arg [ H ( jw)]) ou bien par sa partie réelle et sa partie imaginaire.
1.3.2 Représentation fonctionnelle
Représentation dans le plan de Black : Diagramme de Black :
On représente le gain exprimé en décibels en fonction de la phase en degré pour une même pulsation w . On obtient donc une courbe paramétrée par w .
Cette représentation est très utilisée pour concevoir la correction d’un système. Elle est aussi assez souvent rencontrée dans les sujets de SI en Classe Préparatoire aux Grandes Ecoles.
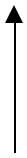

 H ( jw )
H ( jw ) 
 dB = H dB (w)
dB = H dB (w)
Page 3 Emmanuel FARGES Ó EduKlub S.A.
Tous droits de l’auteur des œuvres réservés. Sauf autorisation, la reproduction ainsi que toute utilisation des œuvres autre que la consultation individuelle et privée sont interdites.
Sciences Indusrielles
Systèmes linéaires continus invariants
ANALYSE FREQUENTIELLE
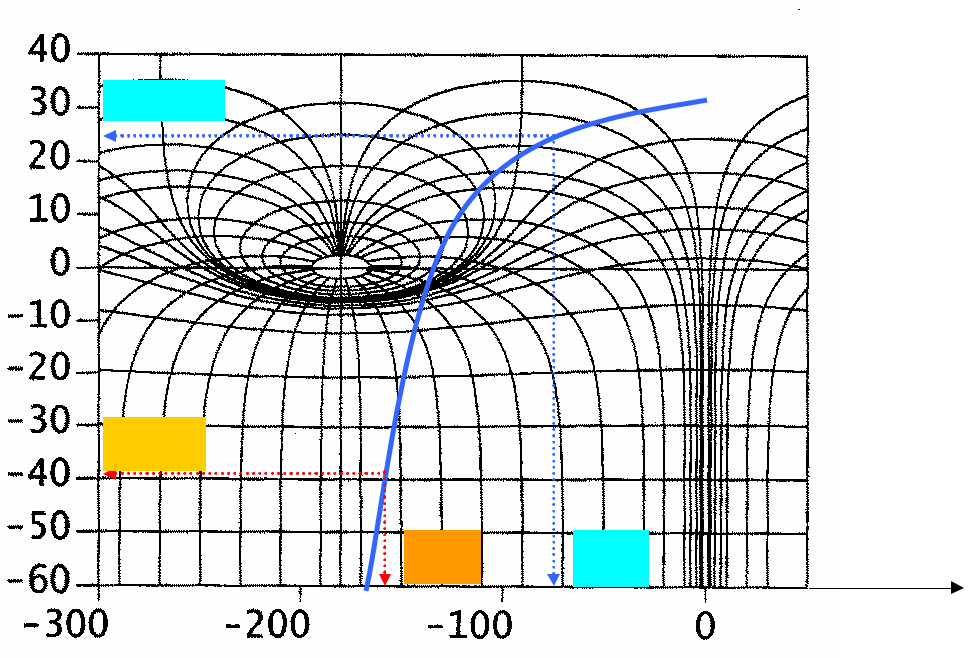
H dB (w1)
H dB (w2 )
j (w2 ) j (w1 ) j (w )
Représentation dans le plan de Bode : Diagrammes de Bode
On représente le gain du système en fonction de la pulsation w sur une courbe avec une échelle logarithmique en abscisse (voir exemple ci-dessous).
On représente la phase du système en fonction de la pulsation w sur une autre courbe avec toujours l’échelle logarithmique pour les pulsations w (voir exemple ci-dessous).
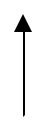
H dB(w)
Page 4 Emmanuel FARGES Ó EduKlub S.A.
Tous droits de l’auteur des œuvres réservés. Sauf autorisation, la reproduction ainsi que toute utilisation des œuvres autre que la consultation individuelle et privée sont interdites.
Sciences Indusrielles
Systèmes linéaires continus invariants
ANALYSE FREQUENTIELLE
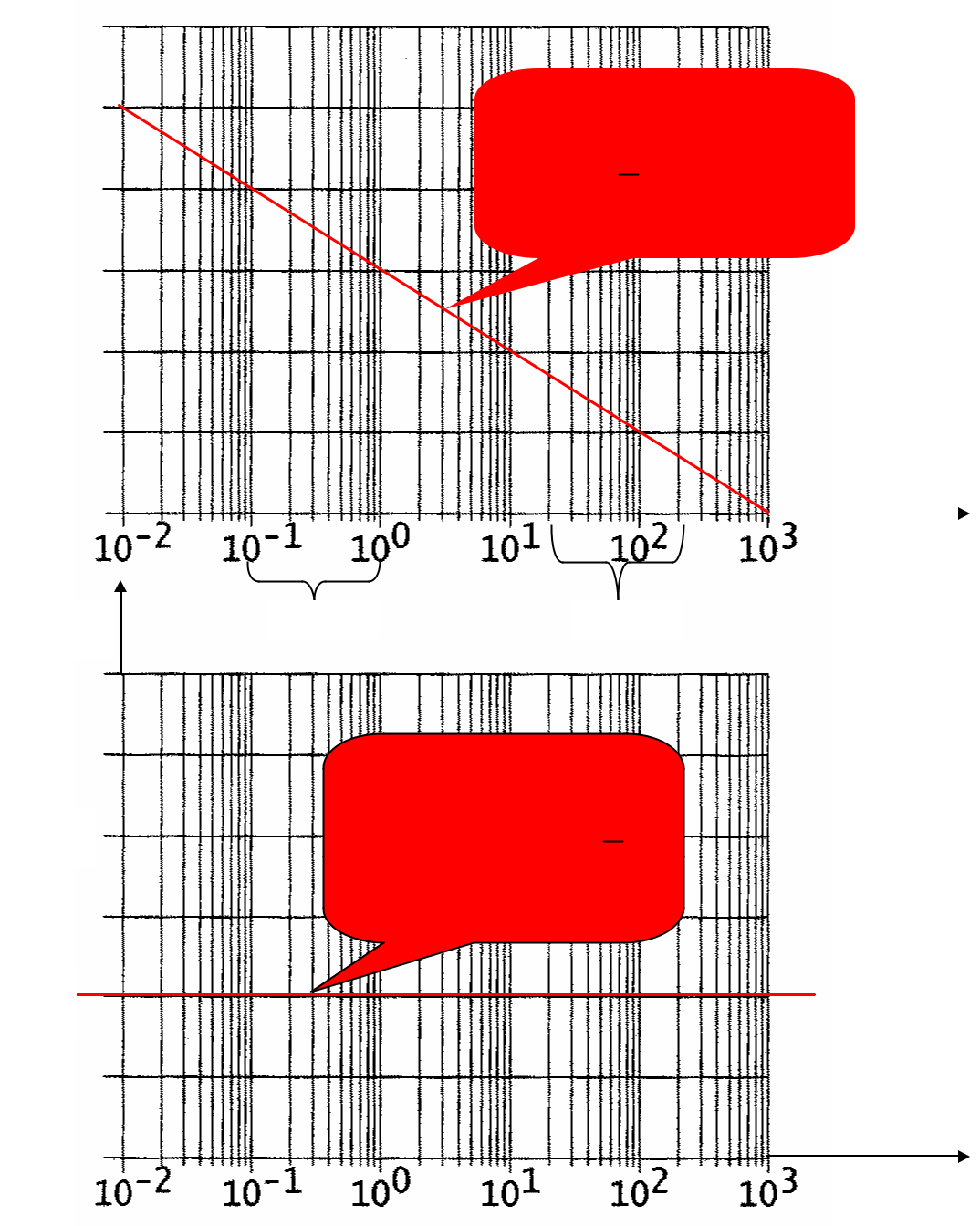
- dB
0 dB
- (w )
0°
Droite de pente -20dB/décade
correspondant à lafonction de
transfert : 1 ,c’est à dire au
p
gain : H dB (w ) = -20Logw
w (rad s-1 )
1 décade 1 décade
Droite horizontale à -90°
correspondant à la phase de
1
la fonction de transfert ,
c’est à dire j (w ) = -90°
-90°
w (rad s-1 )
Représentation dans le plan de Nyquist :
On trace la courbe paramétrée par la pulsation w avec en abscisse, la partie réelle du complexe H ( jw) et en ordonnée la partie imaginaire du complexe H ( jw) .
Page 5 Emmanuel FARGES Ó EduKlub S.A.
Tous droits de l’auteur des œuvres réservés. Sauf autorisation, la reproduction ainsi que toute utilisation des œuvres autre que la consultation individuelle et privée sont interdites.
Sciences Indusrielles
Systèmes linéaires continus invariants
ANALYSE FREQUENTIELLE
Ce type d’étude dans le plan dit de Nyquist n’est pas très fréquemment rencontré dans les sujets de concours aux écoles d’ingénieurs.
Im éë H ( jw )ùû
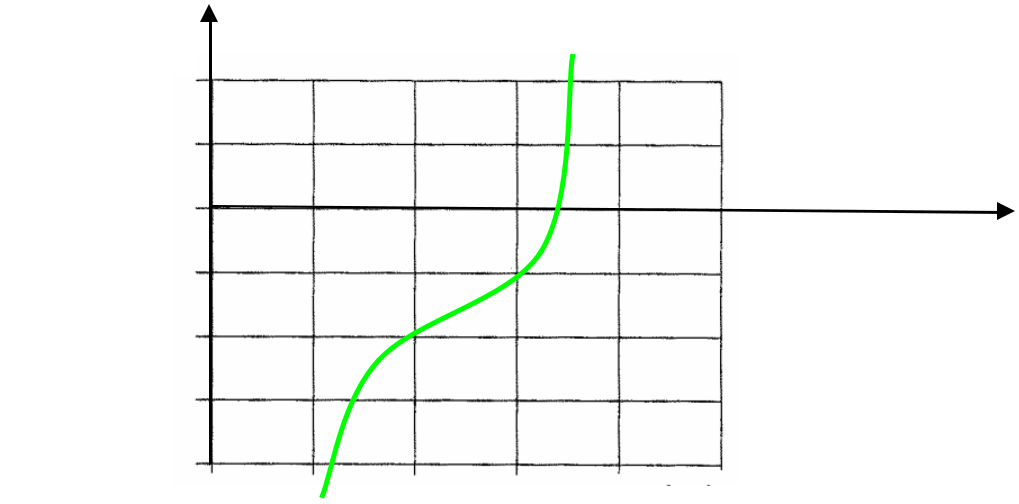
Re éë H ( jw )ùû
1.3.3 Asymptote dans les diagrammes de Bode
Rechercher des asymptotes pour les courbes de Bode revient à chercher des équivalents pour
K
les fonctions de transfert sous la forme : H ( p ) = .
En effet les systèmes qui répondent à cette forme de fonction de transfert ( n = 0 : H(p) modélise un gain pur, n Î ¥ * + : intégrateurs, n Î¥ * – : dérivateurs), ont des diagrammes de Bode réels qui sont des droites.
On pose p = jw et on s’intéresse au module et à l’argument du complexe H ( jw)
|
K æ 1 ön |
æ |
p ön |
p |
|||||||||||||||||||||||||||||||||
|
K |
K |
(- j )n |
K |
ç – j |
÷ |
K |
– jn |
|||||||||||||||||||||||||||||
|
H ( jw) = |
= |
ç |
÷ = |
= |
ç e |
2 ÷ |
= |
e |
2 |
|||||||||||||||||||||||||||
|
n |
n |
n |
n |
|||||||||||||||||||||||||||||||||
|
( |
) |
n è j ø |
( ) |
( |
ç |
÷ |
( |
) |
||||||||||||||||||||||||||||
|
jw |
( ) |
w |
) |
w |
||||||||||||||||||||||||||||||||
|
w |
w |
è |
ø |
|||||||||||||||||||||||||||||||||
|
On vient donc de mettre en forme H ( jw) de manière à faire apparaître son |
||||||||||||||||||||||||||||||||||||
|
module : |
H ( jw) |
= |
K |
et son argument, c’est à dire la phase de la fonction de |
||||||||||||||||||||||||||||||||
|
wn |
||||||||||||||||||||||||||||||||||||
p
transfert : j (w) = –n 2 . Le module en dB est donc : H ( jw ) dB = 20LogK – 20 nLogw ,
c’est à dire une droite de pente -20n dB décade passant par le point (w = 1, 20LogK )

En effet l’échelle de pulsation en abscisse étant logarithmique, une droite y a pour équation :
y = a L og w + b .
Page 6 Emmanuel FARGES Ó EduKlub S.A.
Tous droits de l’auteur des œuvres réservés. Sauf autorisation, la reproduction ainsi que toute utilisation des œuvres autre que la consultation individuelle et privée sont interdites.
Sciences Indusrielles
Systèmes linéaires continus invariants
ANALYSE FREQUENTIELLE
On obtient donc les diagrammes de Bode suivants pour
H dB (w)
20logK
20LogK-40n (2décade s d’écart)
j (w )
0
- n p
2
K
H ( p ) =
Droite d’équation :
20LogK – 20nLogw :
Droite de pente -20n dB /décade passant par le point (w = 1;20LogK )
w (rad s-1 )
w (rad s-1 )
1.3.4 Notions importantes
1.3.4.1 Pulsation au gain unité
Définition : La pulsation au gain unité est la pulsation pour laquelle le gain du système (c’est à dire le module de sa fonction de transfert) vaut 0 dB. Cette pulsation au
gain unité est notée wc0

 H ( jw c 0 )
H ( jw c 0 ) 
 dB = 0 d B Û
dB = 0 d B Û 
 H ( jwc 0 )
H ( jwc 0 ) 
 =1
=1
- Graphiquement, wc0 est la pulsation où le diagramme de Bode en gain coupe les abcisses (0 dB) :
Exemple :
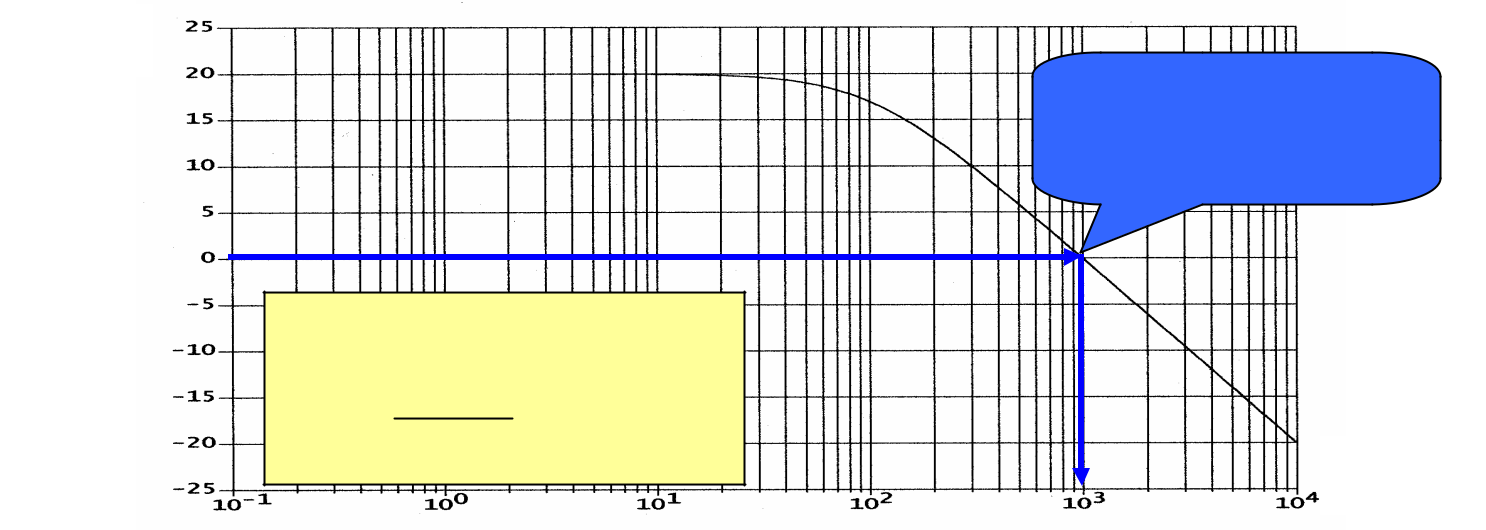
H dB (w)
Pulsation au gain unité ou
pulsation de coupure à
0dB : ici wc0 =1000 rad s-1
Diagramme de Bode en gain du
système de fonction de transfert :
10
H ( p) =
1+ 0,01p
w (rad s-1 )
Page 7 Emmanuel FARGES Ó EduKlub S.A.
Tous droits de l’auteur des œuvres réservés. Sauf autorisation, la reproduction ainsi que toute utilisation des œuvres autre que la consultation individuelle et privée sont interdites.
Sciences Indusrielles
Systèmes linéaires continus invariants
ANALYSE FREQUENTIELLE
1.3.4.2 Bande passante
Définition : La bande passante est définie à partir de ou des pulsations de coupure à un
certain nombre de dB notés l , on la note : wc – ldB

|
çl |
÷ |
|||||||||||||||||||||||||
|
H (0) |
æ |
20 |
ö |
|||||||||||||||||||||||
|
ç |
÷ |
|||||||||||||||||||||||||
|
H (0) |
dB – |
H ( jw c –ldB ) |
dB = l dB Û |
= 10è |
ø |
|||||||||||||||||||||
|
H ( jwc –ldB ) |
||||||||||||||||||||||||||
|
14243 |
||||||||||||||||||||||||||
- LogK
- Graphiquement, wc – ldB est la pulsation à partir de laquelle le diagramme de Bode
en gain est en-dessous de 
 H (0)
H (0) 
 dB – l = 20LogK – l :
dB – l = 20LogK – l :
Exemple :
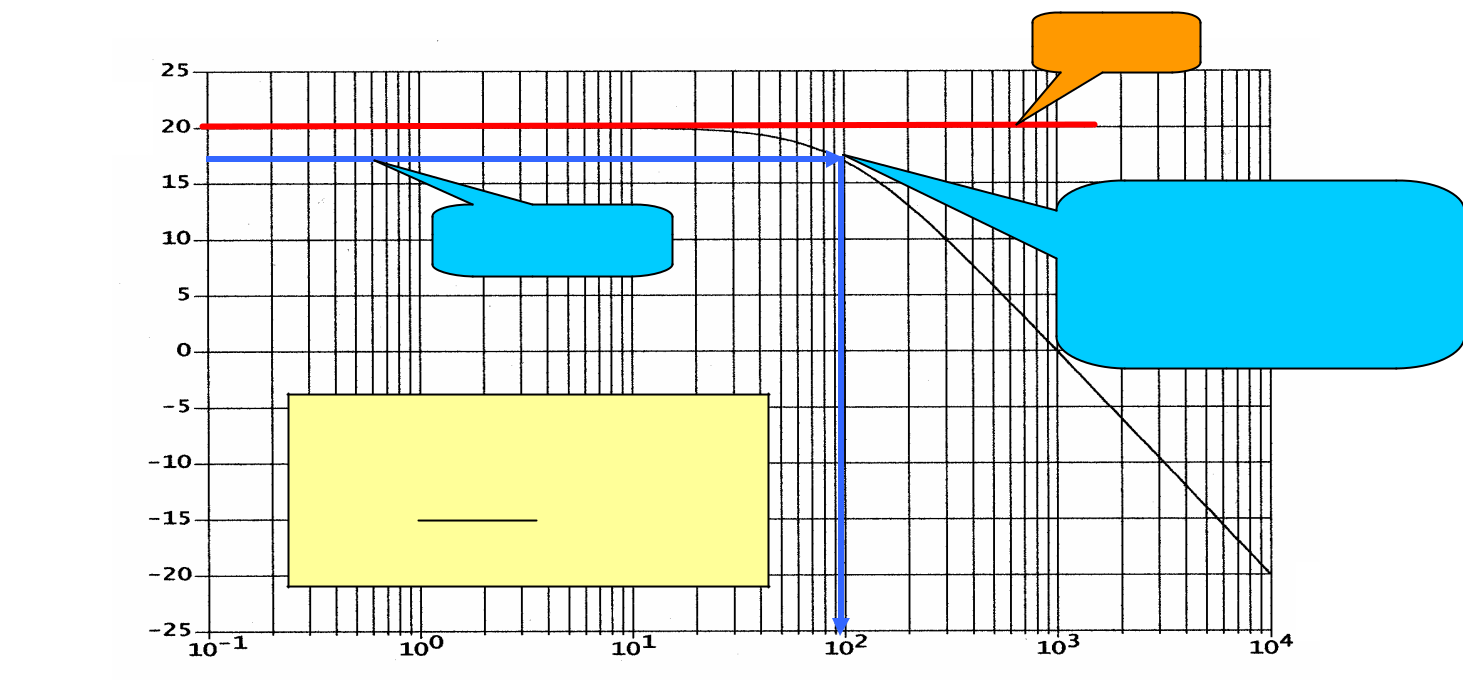
H dB (w)
20LogK – 3dB
Diagramme de Bode en gain du
système de fonction de transfert :
10
H ( p) =
1+ 0,01p
20LogK
Bande passante (ici à -3dB) ou pulsation de coupure à -3dB : ici
wc – 3dB = 100 r a d s-1
w (rad s-1 )
1.3.4.3 Résonnance-Surtension
Définition : On parle de phénomène de résonance dès que la courbe de gain du diagramme de Bode présente un extremum (maximum avec tangente nulle : autre que la tangente nulle de l’asymptote horizontale 20Log K pour w ® 0 ).
- La pulsation pour laquelle existe ce maximum est appelée pulsation de résonance et est notée : wr
- La surtension notée Q (QdB lorsqu’elle est exprimée en dB) quantifie le pic de résonance. En dB c’est l’écart entre le pic de résonance et le gain statique en dB.
|
QdB = |
H (jw r ) |
– |
H (0) |
dB |
= |
H (jwr ) |
– 20LogK |
|||||||
|
dB |
dB |
|||||||||||||
Page 8 Emmanuel FARGES Ó EduKlub S.A.
Tous droits de l’auteur des œuvres réservés. Sauf autorisation, la reproduction ainsi que toute utilisation des œuvres autre que la consultation individuelle et privée sont interdites.
Sciences Indusrielles
Systèmes linéaires continus invariants
ANALYSE FREQUENTIELLE
Exemple :
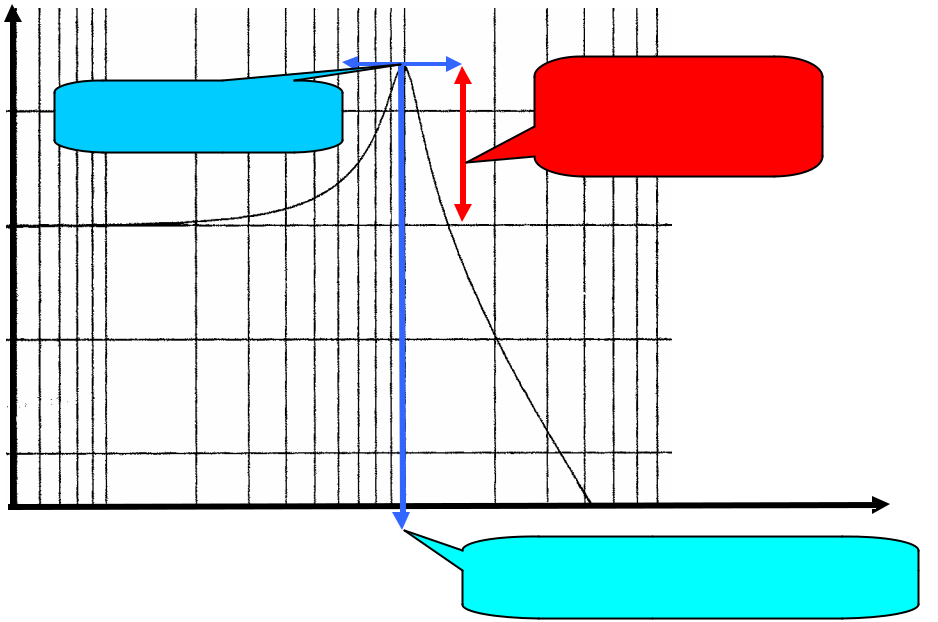
H dB (w)
|
Pic de résonance |
Coefficient de |
|
|
surtension QdB |
||
20LogK
w (rad s-1 )
Pulsation de résonance wr
2 Système du premier ordre.
2.1 Définition d’un système du premier ordre
Un système du premier ordre a son comportement régi par une équation différentielle du premier ordre de la forme :
|
ì |
e = e(t ) entréedusystème |
||||
|
ds |
ï |
s = s (t ) réponsedusystèmeàl’entréee(t) |
|||
|
s +t |
= Ke |
ï |
|||
|
í |
K:gainstatique(>0) |
||||
|
dt |
|||||
|
ï |
ïît :constantedetemps(>0,homogèneà untemps(seconde (s))
2.2 Fonction de transfert globale d’un premier ordre
On applique la transformée de Laplace à l’ensemble de l’équation différentielle ci-dessus, avec des conditions initiales nulles :
Rappel : La transformée de Laplace d’une fonction f(t) est une fonction de p, notée par
convention avec la lettre majuscule de la fonction du temps transformée : F(p)
Donc : s +t ds = Ke transforméedeLaplace S + t pS = KE
dt uuuuuuuuuuuuuuuuuuuuuuuuuuru
On peut alors présenter le rapport de la sortie S(p) sur l’entrée E(p), c’est à dire la fonction de
|
transfert globale du système : |
H ( p) = |
S( p ) |
= |
K |
||
|
1+t p |
||||||
|
E( p) |
||||||
Page 9 Emmanuel FARGES Ó EduKlub S.A.
Tous droits de l’auteur des œuvres réservés. Sauf autorisation, la reproduction ainsi que toute utilisation des œuvres autre que la consultation individuelle et privée sont interdites.
Sciences Indusrielles
Systèmes linéaires continus invariants
ANALYSE FREQUENTIELLE
On note :
- Le gain statique vaut : K=H(0)
- Pour identifier les caractéristiques d’un système du premier ordre (c’est à dire K et t ), on veillera bien à présenter la fonction de transfert globale H(p) avec le
coefficient en p0 du polynôme au dénominateur égal à 1. Ainsi le numérateur peut être identifié au gain statique K et le coefficient en p1 du polynôme au dénominateur peut être identifié à la constante de temps t
2.3 Gain et phase réels d’un premier ordre
|
H ( jw) = |
K |
||
|
1+ jtw |
|||
|
Calcul du gain : |
|||
|
H ( jw) = |
K |
soit en dB : H ( jw ) dB = 20Log H ( jw) |
|
|
1 +t 2 w2 |
|||
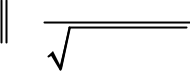

 H ( jw)
H ( jw) 
 dB = 20LogK – 20 Log
dB = 20LogK – 20 Log 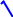
 1 +t 2 w2
1 +t 2 w2

Calcul de la phase :
- (w ) = Arg [ H ( jw)]
|
H ( jw) = |
K |
= |
K(1- jtw) |
= |
K |
1 – jtw |
) |
, donc : |
|||||||
|
2 2 |
|||||||||||||||
|
( |
)( |
) |
( |
||||||||||||
|
1 + jtw |
+ jtw |
– jtw |
1 |
+t w |
|||||||||||
|
1 |
1 |
||||||||||||||
- (w ) = Arg [ H( jw) ] = Arg [1- jtw]
|
( |
– jtw |
) |
( |
) |
( |
) |
||||||||||||||||||||||||
|
tan j = |
Im 1 |
;cosj = |
Re 1- jtw |
;sinj = |
Im 1- jtw |
|||||||||||||||||||||||||
|
Re 1 |
– jtw |
) |
1 – jtw |
1- jtw |
||||||||||||||||||||||||||
|
( |
||||||||||||||||||||||||||||||
|
Donc : |
||||||||||||||||||||||||||||||
|
tan j = |
–tw |
;cosj = |
1 |
;sinj = |
–tw |
|||||||||||||||||||||||||
|
1 |
1+ t 2w 2 |
1+t 2w2 |
||||||||||||||||||||||||||||


- (w) = – arctan [tw]
2.4 Asymptotes des diagrammes de Bode
Deux méthodes sont possibles pour déterminer les asymptotes des diagrammes de Bode : Soit on détermine les équivalents en 0 et en +¥ du gain réel et de la phase réelle, soit on cherche des équivalents directement sur la fonction de transfert.
1ère méthode : équivalents à partir des fonctions de gain et de phase réels.
Asymptote sur le diagramme de gain :


 H ( jw)
H ( jw) 
 dB = 20LogK – 20 Log
dB = 20LogK – 20 Log 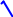
 1 +t 2 w2 est la fonction du ga in (en dB) réelle
1 +t 2 w2 est la fonction du ga in (en dB) réelle

- équivalent lorsque w ® 0 : on peut négliger le terme en t 2w2 devant1.Donc :
|
H ( jw) |
; 20LogK |
, c’est une droite horizontale d’ordonnée 20LogK dB. |
||||
|
{ |
||||||
|
dB w ® 0 |
Ó EduKlub S.A. |
|||||
|
Page 10 |
Emmanuel FARGES |
|||||
Tous droits de l’auteur des œuvres réservés. Sauf autorisation, la reproduction ainsi que toute utilisation des œuvres autre que la consultation individuelle et privée sont interdites.
Sciences Indusrielles
Systèmes linéaires continus invariants
ANALYSE FREQUENTIELLE
- équivalent lorsque w ® ¥ : on peut négliger le terme en 1devant t 2w 2 .Donc :
|
H ( jw) |
; 20LogK – 20Logtw , soit, mis en forme différemment pour faire |
|
{ |
|
|
dB w ® ¥ |
clairement apparaître la pente de la droite :
|
H ( jw) |
; 20LogK – 20 Logt |
-20 |
Logw |
c’est une |
|||||
|
{ |
{ |
||||||||
|
dB w ® ¥ |
pentedeladroiteasymp to te |
||||||||
|
droite de pente -20 dB |
décade |
passant par le point |
(w = 1; |
20LogK – 20Logt ). |
|||||

Intersection entre les deux asymptotes :
On cherche la pulsation dite pulsation propre du système notée w p pour laquelle les deux asymptotes ont des valeurs égales. L’équation permettant de déterminer w p est donc :
20LogK = 20LogK – 20Logt – 20Logw p .
1
Soit 20Logw p = -20Logt ; d’où :w p = t
Explication sur la pente de la droite et la notion de décade :
Un décade est une plage fréquentielle contenue entre une pulsation w0 et 10 fois sa valeur : 10w0 . Donc les deux points qui correspondent à ces pulsations sur l’asymptote sont : (w0 ; 20LogK – 20Logt – 20Logw0 )et
|
æ |
ö |
||
|
ç |
-20Log (10w0 ) |
÷ |
|
|
ç 10w0 ;20LogK – 20Logt |
÷. Ils y a donc un écart de -20 dB entre |
||
|
ç |
1442443 |
÷ |
|
|
ç |
= – 20Logw – 20 |
÷ |
|
|
è |
0 |
ø |

les deux points séparées d’une décade, d’où la pente de -20 dB décade .
Asymptote sur le diagramme de phase :
|
La fonction de phase réelle est définie par |
tan j = |
–tw |
;cosj = |
1 |
;sinj = |
–tw |
|||||
|
1 |
1+ t 2w 2 |
1+t 2w2 |
|||||||||


- (w) = – arctan [tw]
- équivalent lorsque w ® 0 : j (w ) » 0°.Donc, on a une asymptote horizontale à 0°
|
Ø |
équivalent lorsque w ® ¥ |
( |
) |
p |
( |
) |
||||
|
: j w |
» – |
– 90° |
.Donc, on a une asymptote |
|||||||
|
2 |
||||||||||
horizontale à -90°
Page 11 Emmanuel FARGES Ó EduKlub S.A.
Tous droits de l’auteur des œuvres réservés. Sauf autorisation, la reproduction ainsi que toute utilisation des œuvres autre que la consultation individuelle et privée sont interdites.
Sciences Indusrielles
Systèmes linéaires continus invariants
ANALYSE FREQUENTIELLE
|
Comme |
æ |
ö |
æ |
1 |
ö |
= -arctan (1) = – |
p |
(- 45°) |
, on relie les deux asymptotes qui sont |
|
|
j ç w |
÷ |
= j ç |
÷ |
4 |
||||||
|
è |
p ø |
è t |
ø |
|||||||
normalement parallèles (puisque toutes les deux horizontales) au niveau de la pulsation propre
1
du système w p = t .
2ème méthode : équivalents à partir de la fonction de transfert :
A
On cherche des équivalents de la fonction de transfert de la forme
pn
Fonction de transfert équivalente pour w ® 0 , c’est à dire pour p ® 0 (puisque p = jw )
|
H ( p ) = |
K |
équivalentà |
K |
soit |
K |
|||
|
1 |
0 |
|||||||
|
1 +t p |
14243 |
p |
||||||
|
quand p ® 0 |
||||||||
- On retrouve donc l’asymptote horizontale pour w ® 0 à 20LogK pour la courbe de gain en dB (d’après les résultats démontrés paragraphe 1.3.3)
- On retrouve donc l’asymptote horizontale pour w ® 0 à 0° pour la courbe de phase (d’après les résultats démontrés paragraphe 1.3.3)
Fonction de transfert équivalente pour w ® ¥ , c’est à dire pour p ® ¥ (puisque p = jw )
|
K |
K |
K |
|||||||
|
H ( p) = |
équivalentà |
soit |
t |
||||||
|
+t p |
t p |
1 |
|||||||
|
1 |
14243 |
||||||||
|
quand p ® ¥ |
p |
||||||||

- On retrouve donc l’asymptote de pente -20dB/décade pour w ® ¥ à
20Log Kt – (20 ´ 1)Logw = 20LogK – 20Logt – 20Logw pour la courbe de gain en dB (d’après les résultats démontrés paragraphe 1.3.3)
ü On retrouve donc l’asymptote horizontale pour w ® ¥ à – p (-90°) pour la courbe 2
de phase (d’après les résultats démontrés paragraphe 1.3.3)
Page 12 Emmanuel FARGES Ó EduKlub S.A.
Tous droits de l’auteur des œuvres réservés. Sauf autorisation, la reproduction ainsi que toute utilisation des œuvres autre que la consultation individuelle et privée sont interdites.
Sciences Indusrielles
Systèmes linéaires continus invariants
ANALYSE FREQUENTIELLE
Graphiquement cela donne les diagrammes asymptotiques schématiques suivants :
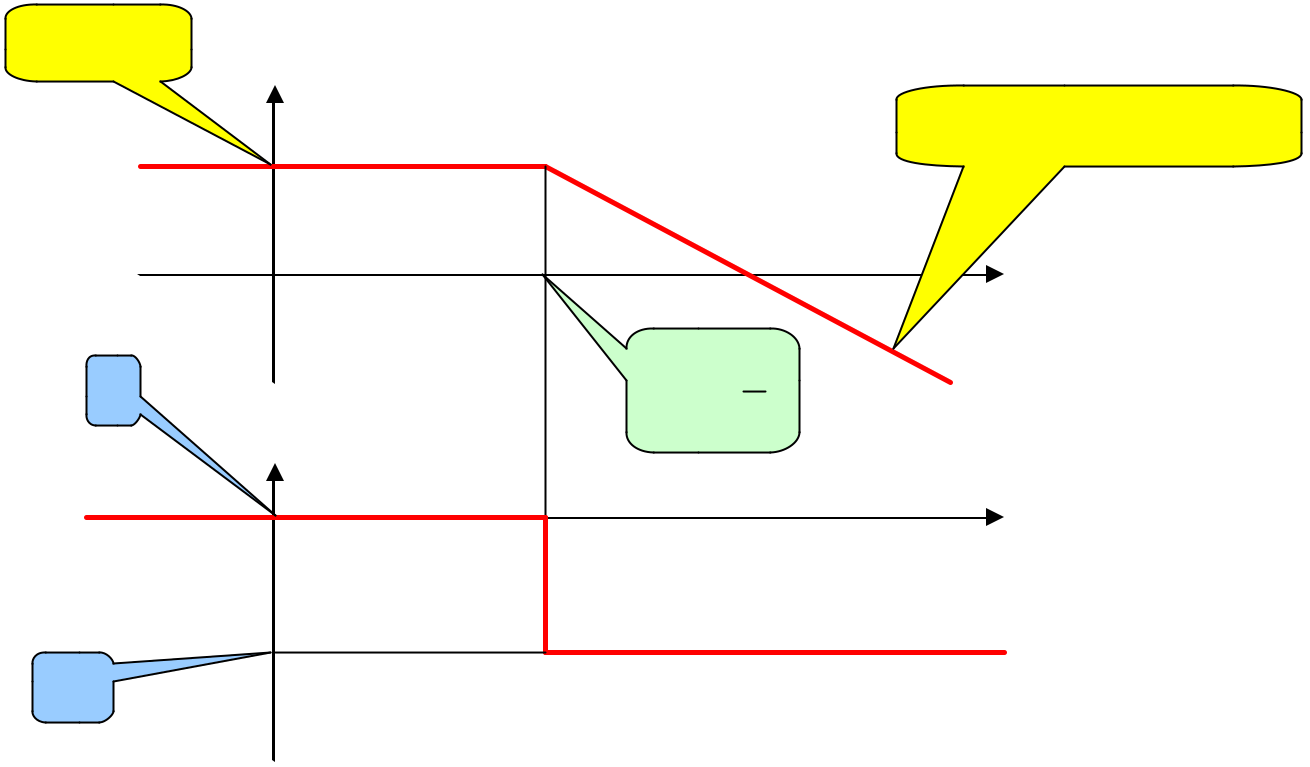
|
20LogK |
H dB |
(w) |
|
Pente : -20 dB / décade
w
|
0° |
w p = |
1 |
||
|
j w |
t |
|||
|
( |
) |
w
-90°
2.5 Diagrammes de Bode d’un premier ordre
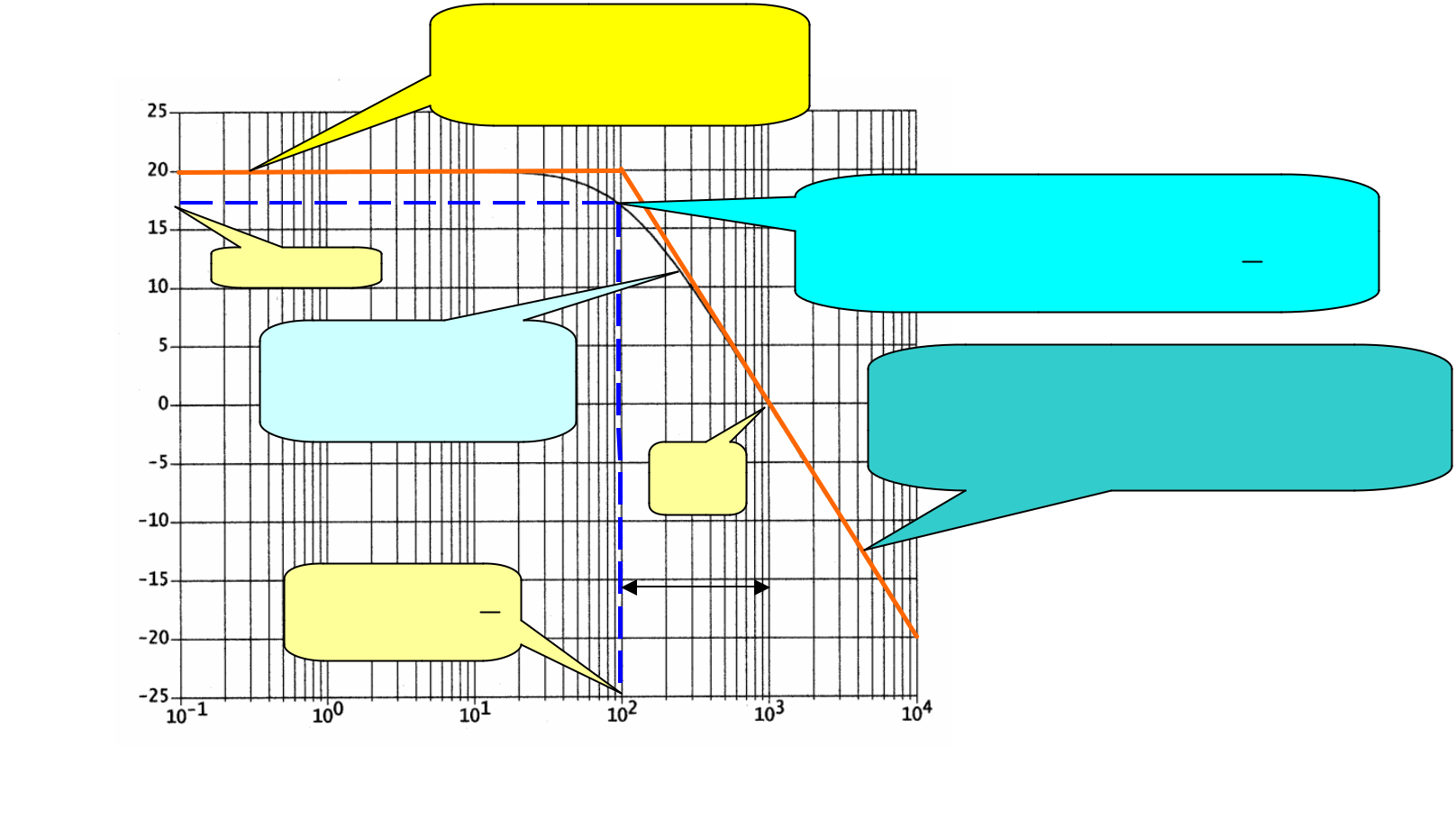
Asymptote horizontale
à 20LogK
H dB (w)
20 – 3= 17dB
Courbe de Gain en
dB réelle.
Pulsation de coupure à -3dB ou bande
1
passante à -3dB : w c -3dB = w p = t
Asymptote de pente : -20 dB/décade, d’équation :
wc 0
20LogK – 20Logt – 20Logw
|
w |
c -3dB |
= w |
p |
= 1 |
||
|
1 décade |
||||||
|
t |
w (r a d s-1 )
- (w )
Page 13 Emmanuel FARGES Ó EduKlub S.A.
Tous droits de l’auteur des œuvres réservés. Sauf autorisation, la reproduction ainsi que toute utilisation des œuvres autre que la consultation individuelle et privée sont interdites.
Sciences Indusrielles
Systèmes linéaires continus invariants
ANALYSE FREQUENTIELLE
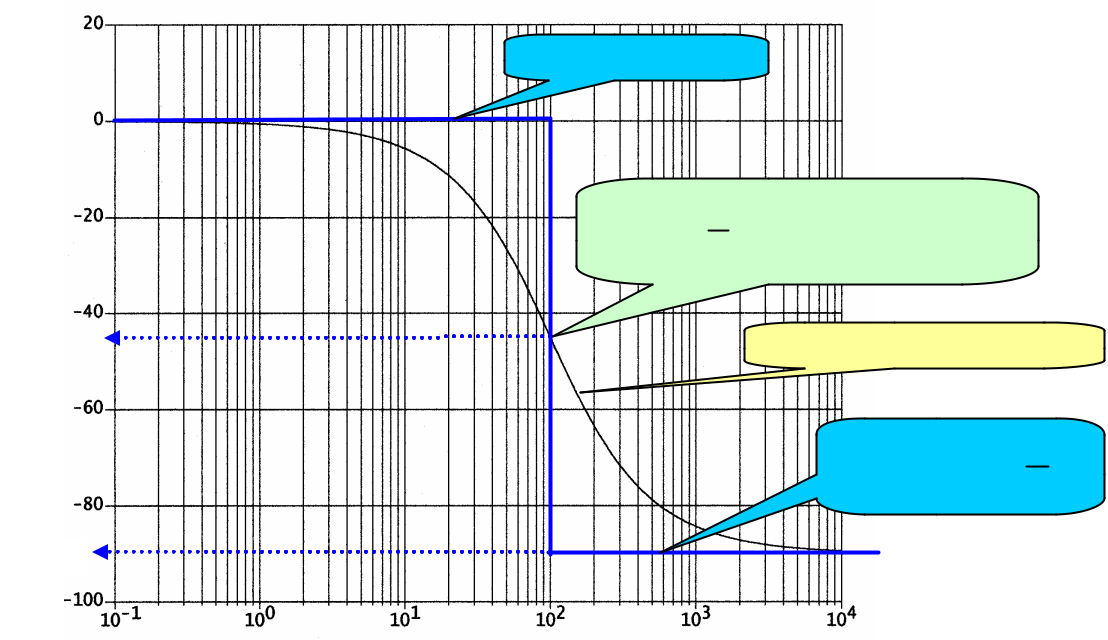
Asymptote à 0°
- æç wp = t1 ö÷ = – arctan (1) = – 45°
èø
Courbe réelle de phase
Asymptote à – p
2
-90°
w (rad s-1 )
Justification de la bande passante à -3dB :
La pulsation de coupure à -3dB ou bande passante à -3dB est telle que :
20 LogK – 
 H ( jwc-3dB )
H ( jwc-3dB ) 
 dB = 3dB , soit pour un premier ordre :
dB = 3dB , soit pour un premier ordre :

20LogK – 20LogK + 20Log 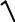
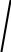 1+ t 2wc2-3dB = 3
1+ t 2wc2-3dB = 3

|
20Log 1 + t 2wc2-3dB |
= |
3 |
|||||||||||||||||||||
|
æ |
3 |
ö |
æ |
6 ö |
|||||||||||||||||||
|
ç |
÷ |
ç |
÷ |
||||||||||||||||||||
|
20 |
20 |
||||||||||||||||||||||
|
2 2 |
=10 |
è |
ø |
Þ 1 |
+t |
2 |
2 |
è |
ø |
; 2 |
2 2 |
= 1 |
|||||||||||
|
1+ t wc -3dB |
wc– 3 dB |
= 10 |
Þt wc -3dB |
||||||||||||||||||||
|
D’où : |
w |
= |
1 |
= w |
|||||||||||||||||||
|
c -3 dB |
p |
||||||||||||||||||||||
|
t |
|||||||||||||||||||||||

Page 14 Emmanuel FARGES Ó EduKlub S.A.
Tous droits de l’auteur des œuvres réservés. Sauf autorisation, la reproduction ainsi que toute utilisation des œuvres autre que la consultation individuelle et privée sont interdites.