Blog

Sciences Indusrielles

Systèmes linéaires continus invariants

Performance des systèmes asservis

SYSTEMES LINEAIRES CONTINUS INVARIANTS

PERFORMANCES DES

SYSTEMES ASSERVIS

1 Stabilité des systèmes asservis

1.1 Notion de stabilité

La stabilité est communément reconnue comme étant associée à la notion d’équilibre :

Prenons les deux positions d’équilibre d’un pendule :

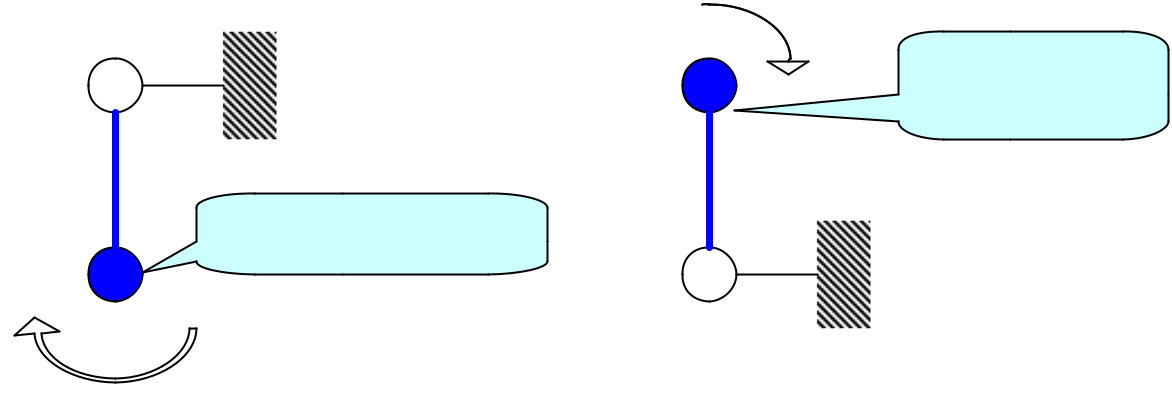
En équilibre

instable

En équilibre stable

A gauche si on écarte le pendule de sa position d’équilibre, il finira par la reprendre.

A droite, si on écarte le pendule de sa position d’équilibre, il s’en écarte définitivement.

On peut élargir cette notion :

Etudions le mouvement d’une bille reposant sur différentes formes.

Equilibre instable		Equilibre stable		Equilibre indifférent

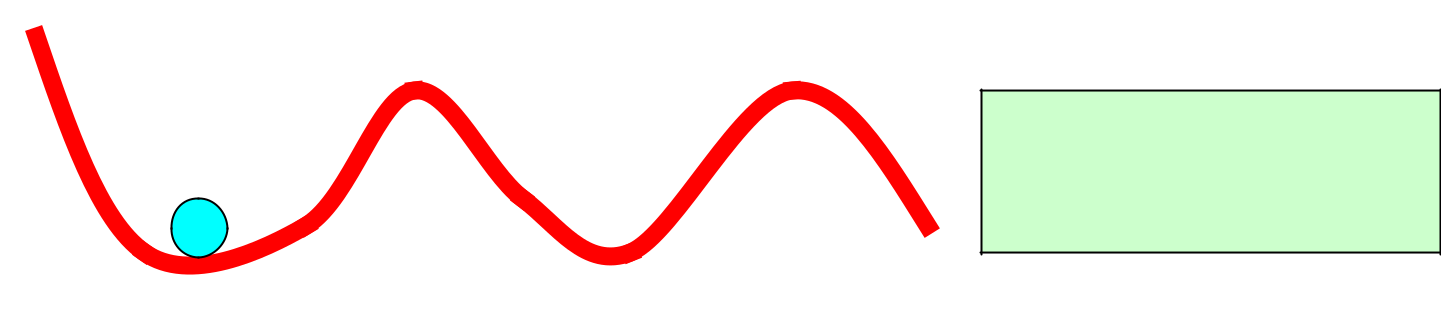
Equilibres multiples stable

et instable suivant le

domaine d’évolution

Il faut donc étudier la qualité de la stabilité d’un système asservis de façon plus précise.

Page 1 Emmanuel FARGES Ó EduKlub S.A.

Tous droits de l’auteur des œuvres réservés. Sauf autorisation, la reproduction ainsi que toute utilisation des œuvres autre que la consultation individuelle et privée sont interdites.

Sciences Indusrielles

Systèmes linéaires continus invariants

Performance des systèmes asservis

1.2 Aspect mathématique

Un système est stable si à toute entrée bornée, le système répond par une sortie bornée

Un système est stable si sa réponse libre (équation différentielle sans second membre) tend vers 0 lorsque le temps tend vers l’infini.

On a vu que toute fonction de transfert et donc en particulier la fo nction de transfert globale d’un système pouvait se mettre après décomposition en éléments simples sous la forme :

H ( p) = å	ci	avec pi Σ les pôles de la fonctions de transfert globale du système.
	p – pi
i

Or après transformée inverse de Laplace, on s’aperçoit que :

• Les pôles nuls engendrent des solutions de la forme t ⁿ (non borné)
• Les pôles réels engendrent des solutions de la forme e^{(pi t )} (borné si p_i < 0)
• Les pôles complexes qui sont nécessairement conjugués engendrent des solutions de la

(Re(pi )t )	sin (w i t +ji ) (borné si Re ( pi ) < 0)
forme : e

La condition générale de stabilité est donc que les pôles de la fonction de transfert globale du système soient à partie réelle strictement négative.

Ce critère est une condition de stabilité mais ne permet pas de quantifier la qualité de cette éventuelle stabilité, ce que nous ferons plus tard.

1.3 Critère algébrique de ROUTH

Ce critère algébrique permet de savoir si un système est stable ou non sans en déterminer la qualité. Il permet de savoir si les zéros d’un polynôme sont à parties réelles négatives ou non. Pour la stabilité on s’intéresse aux pôles de la fonction de transfert, donc aux zéros du

^{N ( p)}

polynôme au dénominateur : D ( p) avec H ( p) =

Posons : D( p) = b_n pⁿ + …….. + b₁ p + b₀

Les zéros de D(p) donc les pôles de la fonction de transfert sont à parties réelles strictement négatives si deux conditions :

Condition 1 : Tous les coefficients b_i sont positifs.

Condition 2 : Tous les coefficients de la première colonne du tableau ci-dessous doivent être positif.

Le tableau se constitue de la façon suivante :

Les deux premières lignes se remplissent avec les coefficients du polynôme D(p).

Les lignes suivantes se déduisent des deux immédiatement précédentes, de la façon suivante :

Page 2 Emmanuel FARGES Ó EduKlub S.A.

Tous droits de l’auteur des œuvres réservés. Sauf autorisation, la reproduction ainsi que toute utilisation des œuvres autre que la consultation individuelle et privée sont interdites.

Sciences Indusrielles

Systèmes linéaires continus invariants

Performance des systèmes asservis

pn

bn

bn-2

bn-4

pn-1

bn-1

bn-3

bn-5

Pn-2

c =

b b

– b b

d =

b b

– b b

etc

n-1 n– 2

n n-3

n-1 n -4

n n-5

bn -1

bn-1

cbn -3 – dbn-1

…

…

c

p1=p

…

…

…

p0=1

…

…

1^ère colonne

Remarque : si les coefficients n’existent pas, on y met des zéros et on ne va pas plus loin.

Remarque : Si un zéro apparaît dans la première colonne, on ne peut plus calculer les autres lignes. On s’intéresse donc aux zéros du polynôme (p+a)D(p) qui a les mêmes zéros que D(p) avec –a en plus. Donc si a>0, cela ne change rien a la stabilité de notre système et cela nous permet d’effectuer les calculs (en général on prend a=1).

1.4 Application à un deuxième ordre

On prend un système représenté par un deuxième ordre à retour unitaire dont le schéma bloc est donné ci-dessous :

E

K

S

+

1+

2x

p +

p2

–

w

w 2

0

0

K

1 +

2x

p + p2

K BF

FTBF =

w0

w02

=

1+

K

1+

2xBF

p + p

2

2x

p2

w02BF

1+

p +

w0BF

w02

w0

K

x

avec

K

BF

=

x

BF

=

w

= w

1+ K

1+ K

1+ K

0 BF

0

Pôles de la fonction de transfert en boucle fermée (FTBF) :

Si xBF	<1
		les pôles sont :	–xBF w0 BF	± jw 0BF		1- xBF2			Re < 0
Si xBF	> 1
		les pôles sont :	–xBF w 0 BF	±w 0 BF	xBF2 -1				< 0

Conclusion : Un deuxième ordre est toujours stable (encore une fois sans notion de qualité de cette stabilité)

Page 3 Emmanuel FARGES Ó EduKlub S.A.

Tous droits de l’auteur des œuvres réservés. Sauf autorisation, la reproduction ainsi que toute utilisation des œuvres autre que la consultation individuelle et privée sont interdites.

Sciences Indusrielles

Systèmes linéaires continus invariants

Performance des systèmes asservis

1.5 Stabilité des systèmes bouclés

On va chercher à quantifier la qualité de cette stabilité en définissant des marges vis-à-vis de la stabilité limite.

On considère le système bouclé classique :

E		S

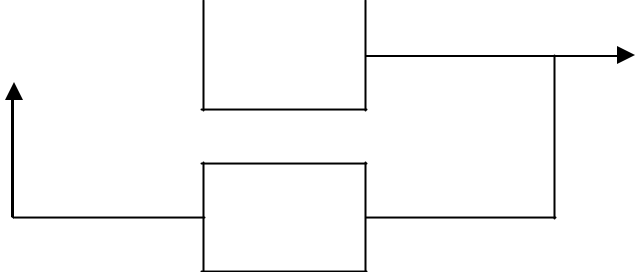
• A(p)

–

B(p)

FTBO = A( p ) B( p)	et	FTBF =	A( p)	=	A( p)
			1+ A( p ) B( p)		1+ FTBO

Faire l’étude de la stabilité de ce système revient à faire l’étude des solutions du polynôme :1 + FTBO = 0 soit FTBO = -1

Donc l’étude de la stabilité se fait dans ce cas sur la FTBO

Le point -1 est appelé point critique

Condition pratique de stabilité : Le but est de s’écarter le plus possible du point critique pour

(^{– jp} ) ^ìH dB ^{= 0dB}

_{lequel : – 1 = e . Soit í}

Marge de Gain :Valeur courante :10dB

On lit la marge de gain sur les diagrammes de Bode de la FTBO

H _dB (w)

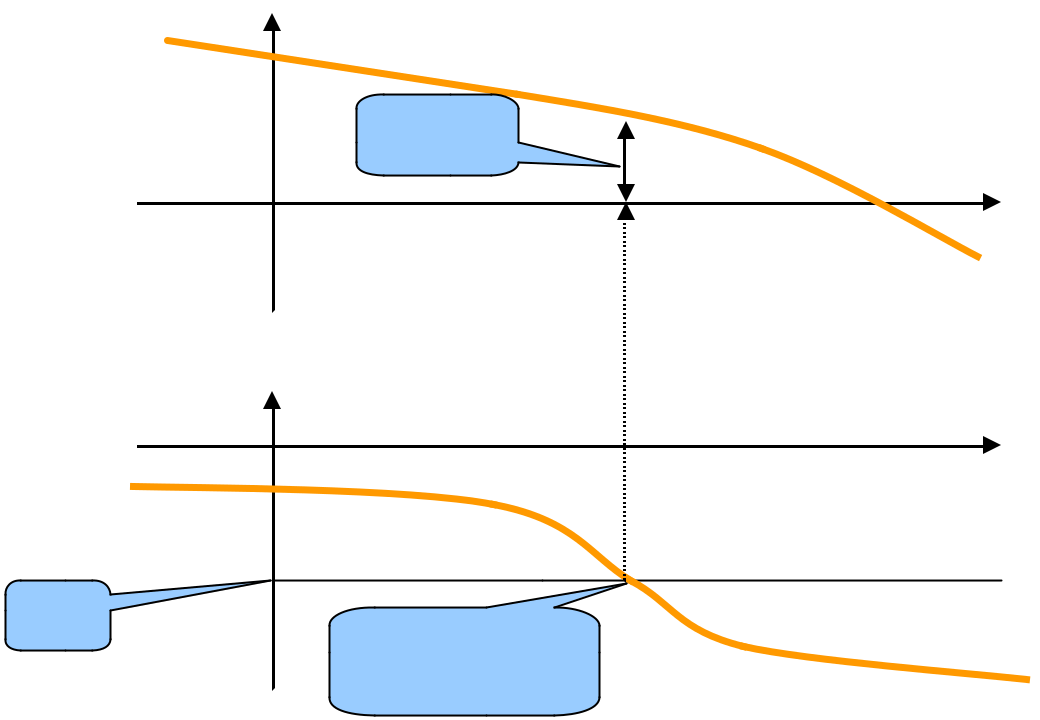
MG < 0

w

j (w )

w

-180°

Point critique

en phase

On se place au point critique sur le diagramme de phase j (w ) = -180° et on lit la

marge de gain sur le diagramme de gain.

La marge de gain est l’écart entre 0dB et le gain au point critique en phase.

• Si on amplifie au point critique, le système est instable : MG<0.
• Si on atténue au point critique , le système est stable avec une marge MG>0

Page 4 Emmanuel FARGES Ó EduKlub S.A.

Tous droits de l’auteur des œuvres réservés. Sauf autorisation, la reproduction ainsi que toute utilisation des œuvres autre que la consultation individuelle et privée sont interdites.

Sciences Indusrielles

Systèmes linéaires continus invariants

Performance des systèmes asservis

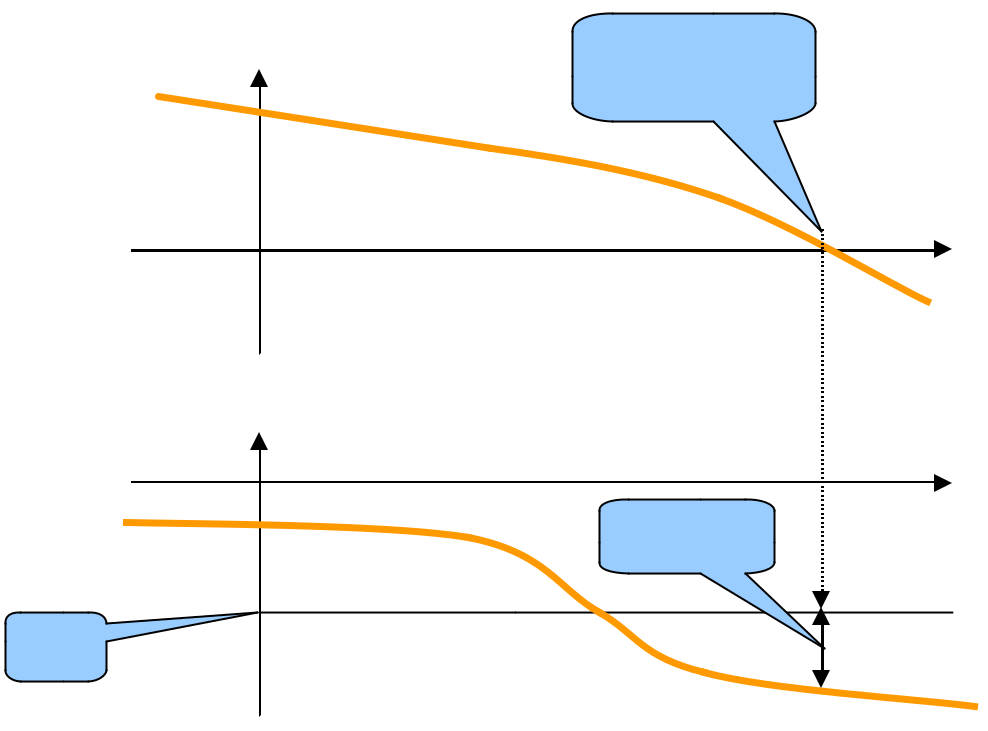
Marge de Phase :Valeur courante 45°

On lit la marge de phase sur les diagrammes de Bode de la FTBO

H dB	(w)	Point critique
		en gain 0 dB

w

j (w )

w

Mj < 0

-180°

On se place au point critique en gain (0 dB) et on lit la marge de phase sur le diagramme de phase La marge de phase Mj est

l’écart en -180° et la phase au point critique en gain.

• Si la phase au point critique en gain est inférieure à -180°, alors le système est instable et Mj < 0
• Si la phase au point critique en gain est supérieure à -180°, le système est stable avec une marge de phase Mj > 0

Marge de phase et de gain sur un diagramme de Black :

Elles sont définies de façons identiques mais se lisent différemment, comme suit :

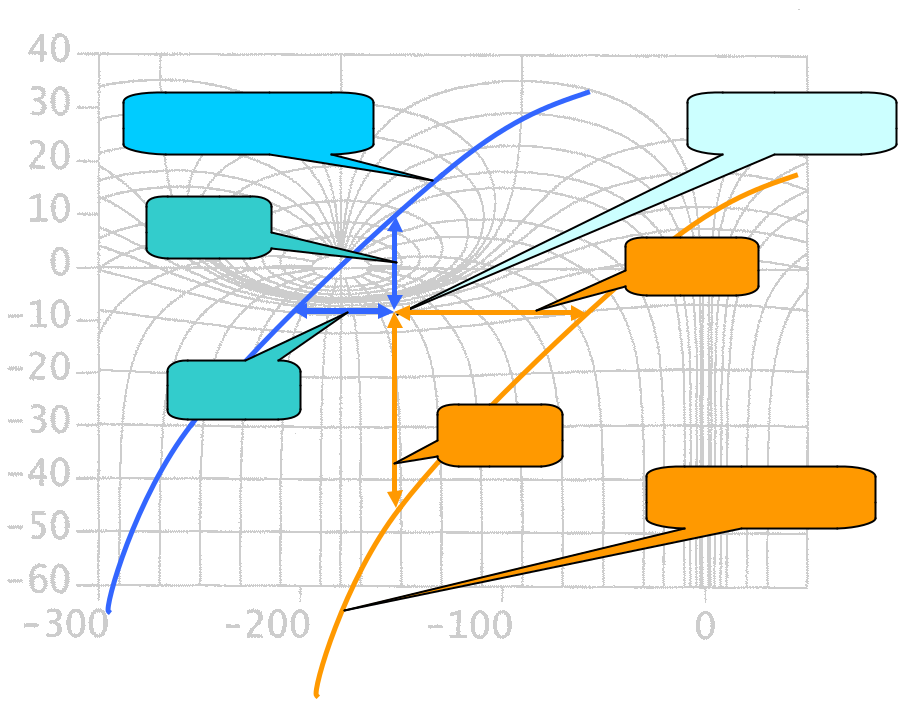
Système instable Point critique

MG<0

Mj > 0

Mj < 0

MG>0

Système stable

Page 5 Emmanuel FARGES Ó EduKlub S.A.

Tous droits de l’auteur des œuvres réservés. Sauf autorisation, la reproduction ainsi que toute utilisation des œuvres autre que la consultation individuelle et privée sont interdites.

Sciences Indusrielles

Systèmes linéaires continus invariants

Performance des systèmes asservis

1. 6 Influence du gain sur la stabilité des systèmes bouclés

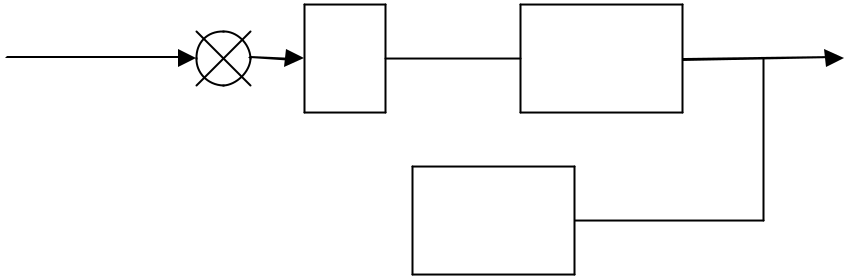
On considère le système bouclé classique avec un correcteur proportionnel K dans la boucle ouverte suivant :

E	+		S
Sans gain dans la boucle ouverte		K	A(p)
la FTBO de ce système vaut :		–
FTBO = A(p) B(p)

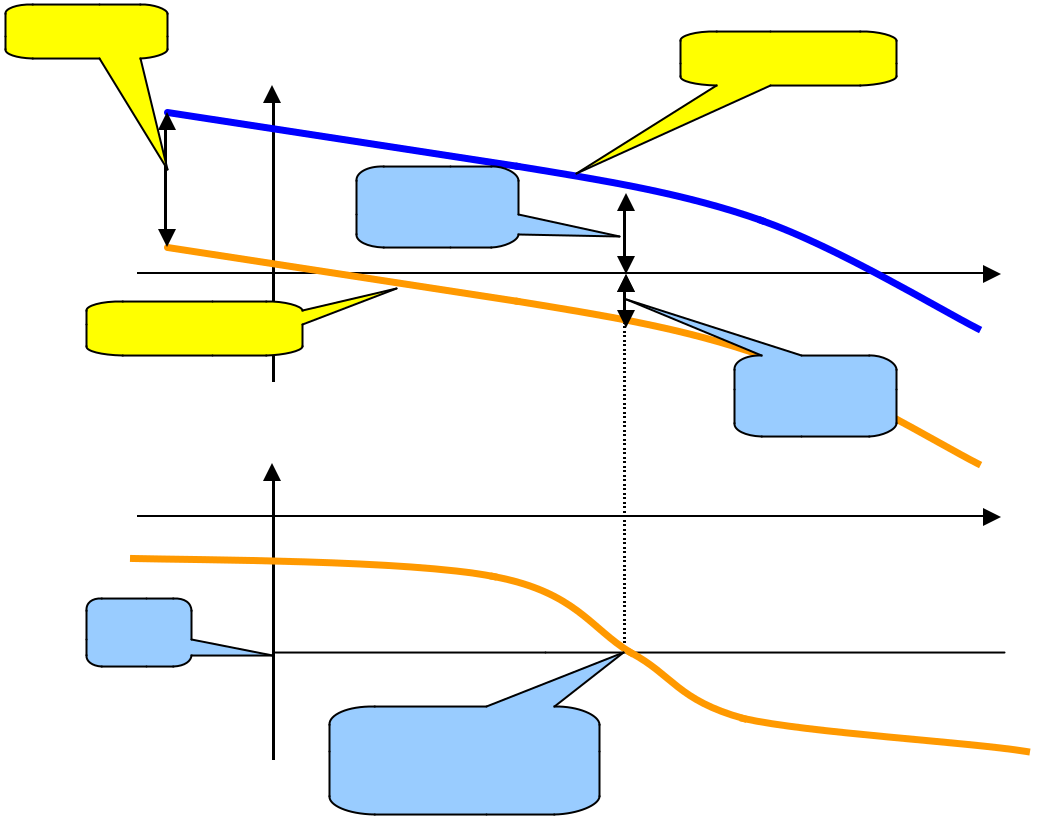
Avec gain dans la boucle ouverte, la

FTBO de ce système devient :

FTBO = K A(p) B(p)

20LogK

B(p)

H (w)

Avec gain K

Si on augmente le gain en boucle ouverte , la phase de la FTBO reste inchangée, alors que le gain est multiplié par K. Cela veut dire que la courbe de phase dans Bode est la même avec ou sans gain alors que la courbe de gain avec gain se déduit de celle sans gain par translation de 20LogK vers le haut :

On passe donc d’un système stable puisque la marge de gain MG est positive à un système instable puisque la marge MG peut devenir négative avec le correcteur proportionnel (K suffisamment grand) dans la boucle ouverte.

Sans gain K

-180°

dB

MG < 0

w

MG > 0

j ( w )

w

Point critique

en phase

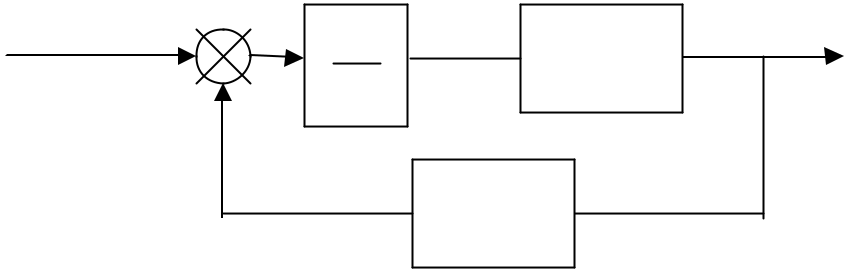
		E	+		1
(	)	dans la		–
					p
Sans intégration a = 0						a

boucle ouverte la FTBO de ce système vaut :FTBO = A(p) B(p)

S

A(p)

B(p)

Page 6 Emmanuel FARGES Ó EduKlub S.A.

Tous droits de l’auteur des œuvres réservés. Sauf autorisation, la reproduction ainsi que toute utilisation des œuvres autre que la consultation individuelle et privée sont interdites.

Sciences Indusrielles

Systèmes linéaires continus invariants

Performance des systèmes asservis

Avec intégration dans la boucle ouverte, la FTBO de ce système

¹

devient : FTBO = A ( p ) B( p)

L’influence de l’action intégrale est très simple sur les courbes de phase des diagrammes de Bode. En effet la phase d’un intégrateur est constante et vaut -90°. Donc les courbes de Bode sont translatées de -90° vers le bas à chaque fois que l’on rajoute un intégrateur.

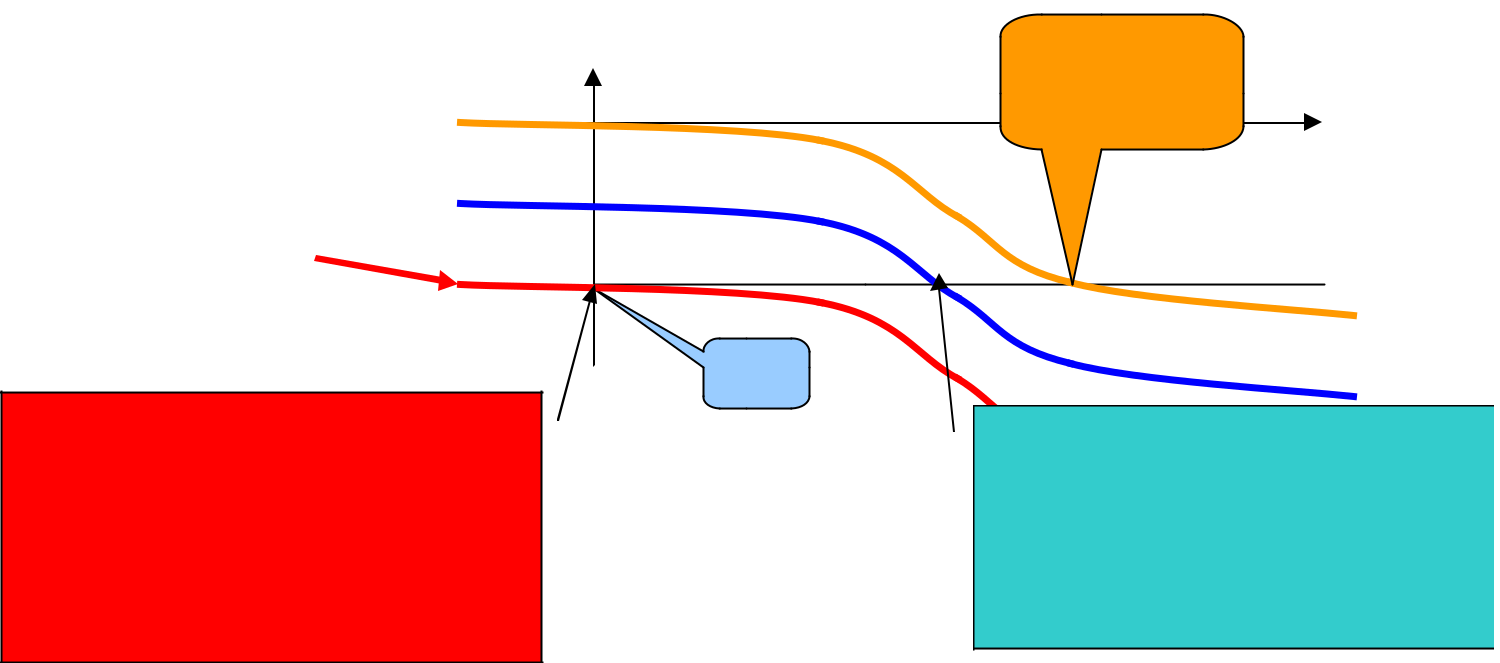
Aucune intégration

Une intégration

Seconde intégration

Point critique en phase avec une double intégration déplacé vers la gauche, c’est à dire vers les zones d’amplification au gain statique a MG ® -20LogK

Le système est déstabilisé

(	)	Point critique
j w
		en phase sans	w
		intégration

-180°

Point critique en phase avec une

intégration déplacé vers la

gauche, c’est à dire vers les

zones d’amplification :

Mauvais pour la stabilité

Conclusion : L’action intégrale dégrade la stabilité des systèmes

2 Précision des systèmes asservis.

2.1 Ecart – Erreur – Précision

La précision caractérise l’écart entre la consigne et la valeur atteinte.

e =	lim	e(t ) – s(t) = lim	p [E( p) – S ( p)]	d’après le théorème de la valeur finale.
	t ® ¥	p ® 0
e =	lim	pE( p)[1 – H ( p)]	avec H ( p) =	FTBF =	S ( p)
					E ( p)
	p ® 0

Considérons un système à retour unitaire pour regarder la précision d’un système.

A( p) = FTBO =	K BO		N ( p)	avec
	pa		D ( p)

pE ( p)

Donc : e = lim

p ®0 1+ FTBO

E+		e	A(p)
	–

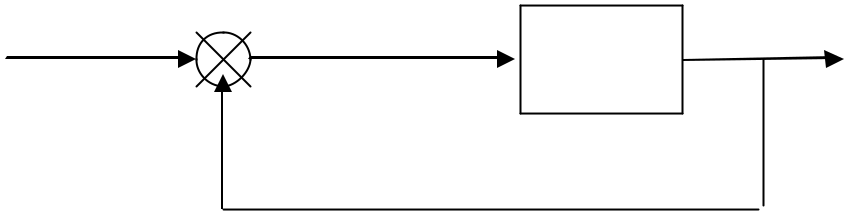
N (0) = D(0) = 0

S

Page 7 Emmanuel FARGES Ó EduKlub S.A.

Tous droits de l’auteur des œuvres réservés. Sauf autorisation, la reproduction ainsi que toute utilisation des œuvres autre que la consultation individuelle et privée sont interdites.

Sciences Indusrielles

Systèmes linéaires continus invariants

Performance des systèmes asservis

2.2 Précision statique

L’erreur statique notée e_s est l’erreur en régime établie pour une entrée de type

^A

échelon : E ( p) =

					A	ì			A	si a = 0:pasd’intégrationenboucleouverte
						ï
Donc :	es	= lim					= í	1	+ KBO
					KBO
		p ®0	1	+		ï			si a ³1:aumoinsunintégrateurenboucleouverte
					a	î0
					p

Conclusion :

• L’erreur statique d’un système bouclé est nulle si on a au moins un intégrateur en boucle ouverte.
• L’erreur statique est d’autant plus faible que le gain en boucle ouverte K_BO est grand quand il n’y a pas d’intégrateur en boucle ouverte.

2.3 Précision dynamique

L’erreur en vitesse ou précision dynamique ou encore erreur de traînage e_s est l’erreur en

régime établi pour une entrée rampe du type E ( p) = ^V p²

					ì			¥ si a=0pasd’intégrateurenboucleouverte
			V		ï			V
					ï
Donc :	et	= lim				= í				si a=1unint égrateur enboucleouverte
				KBO				K
		p®0	p +		ï				BO
				a-1
				p	ï		si a ³ 2 au moinsdeuxintégrateursenboucleouverte
					î0

2.4 Résumé

On peut généraliser la notion de précision en fonction du nombre d’intégrateur dans la boucle ouverte sous forme d’un tableau :

Entrée

Précision, erreur

0 intégrateur

1 intégrateur

2 intégrateur

3 intégrateur

Echelon : A u(t)

Erreur statique

A

0

0

0

1+ K BO

Rampe : V t u(t)

Erreur en vitesse

¥

V

0

0

K BO

Parabole :

Erreur en

¥

¥

g

0

gt 2u (t ) ²

accélération

K BO

2.5 Influence des perturbations

Soit le système perturbé représenté par le schéma bloc ci-dessous :

Page 8 Emmanuel FARGES Ó EduKlub S.A.

Tous droits de l’auteur des œuvres réservés. Sauf autorisation, la reproduction ainsi que toute utilisation des œuvres autre que la consultation individuelle et privée sont interdites.

Sciences Indusrielles

Systèmes linéaires continus invariants

Performance des systèmes asservis

						P
						+
E	+		e						S
					F1(p)		F2(p)
	–					+

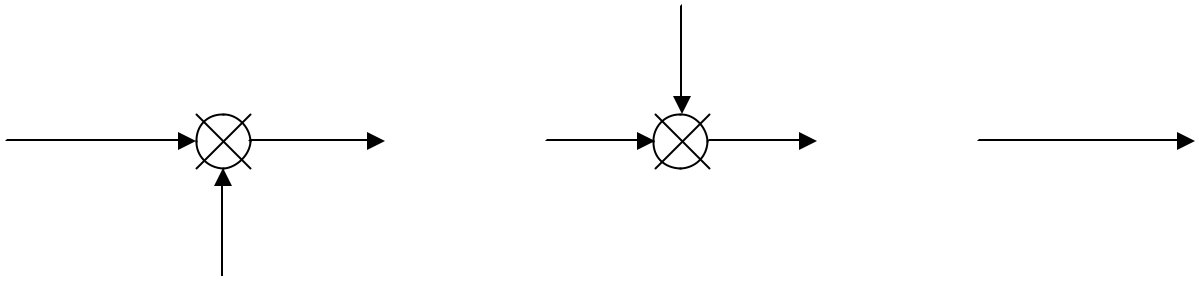
E est l’entrée du système, c’est à dire la consigne

S est la sortie du système, c’est à dire la réponse à l’entrée E

P est une seconde entrée du système appelée perturbation car elle est subie, c’est à dire qu’on ne la maîtrise pas : le vent , la houle, les courant dans le cas d’un pilote automatique de bateau chargé de maintenir le cap de l’embarcation.

• : est l’erreur du système puisque c’est la différence entre l’entrée E (ce que l’on veut faire) et la sortie S (ce que l’on a fait)

Plaçons nous dans le cas général pour les fonctions de transfert F₁ et F₂ :

	K	1		N	( p)		ìN	( p )polynomeen p avec N	(0) = 1
C’est à dire : F ( p) =			1			avec	í 1	1
				D1 ( p)				( p )polynomeen p avec D1 (0) = 1
1	pa1						î D1

Et : F ( p) =

K

2

N

2

( p)

avec

ìN

2

( p)polynomeenpavec N

2

(0)

= 1

í

D 2 (p )

( p)polynomeenpavec D2

2

pa2

î D2

(0)

=1

Il existe deux types d’erreur sur ces systèmes puisque l’on a deux types d’entrées différentes.

On peut donc décomposer l’erreur en deux :

Une erreur vis-à-vis de l’entrée, c’est à dire la consigne (à perturbation nulle) : e₁

Une erreur vis-à-vis de la perturbation (à consigne nulle) : e₂

On a alors : e = e₁ + e₂

Calculons ^e1 :

On peut refaire le schéma bloc avec une perturbation nulle :

e1 = E – S

E

+

e1

S

F1(p) F2(p)

S = F1 F2 e1

–

Donc

e1 =

E

1 + F1 F2

Calculons e2

:

P

On peut refaire le schéma bloc avec une entrée nulle :

+

e2

S

F1(p)

F2(p)

e2 = –S

+

–

S = F2 [

P + F1e

2 ]

Page 9

Emmanuel FARGES

Ó EduKlub S.A.

Tous droits de l’auteur des œuvres réservés. Sauf autorisation, la reproduction ainsi que toute utilisation des œuvres autre que la consultation individuelle et privée sont interdites.

Sciences Indusrielles

Systèmes linéaires continus invariants

Performance des systèmes asservis

D’où : e₂ = – ^{F2 P}

1+ F₁ F₂

Les erreurs vis-à-vis de l’entrée ayant déjà été abordées, on ne s’intéresse ici qu’à l’erreur statique vis-à-vis de la perturbation.

On soumet donc le système à une perturbation échelon (erreur statique), et on regarde quelle

est l’erreur générée : es 2

= lim e

2 (t ) = lim pe

2 ( p)

t ®¥

p®0

e s 2

= lim pe2 ( p) = lim p

P (p )F2 ( p)

avec

P ( p) =

P0

1+ F1 ( p)F2 ( p )

p

p ®0

p®0

es 2

= lim

P K

2

p–a 2

= lim

P K

2

pa1

= lim

P K

2

pa1

0

0

0

+ p(a 1 +a2 )

K 1 K2

p®0 1+ K K p-(a1 +a2 )

p ® 0

K K

2

p®0

1

2

1

Donc si on veut annuler l’erreur statique vis-à-vis d’une perturbation (ce qui est très intéressant étant donnée qu’en général on ne maîtrise pas cette perturbation) : il faut a₁ ³ 1

Conclusion : Pour annuler l’erreur statique vis-à-vis d’une perturbation, il faut placer au moins un intégrateur avant celle-ci.

Page 10 Emmanuel FARGES Ó EduKlub S.A.

Tous droits de l’auteur des œuvres réservés. Sauf autorisation, la reproduction ainsi que toute utilisation des œuvres autre que la consultation individuelle et privée sont interdites.

Telecharger