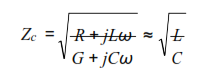1. Caractéristiques techniques des supports.
L’infrastructure d’un réseau, la qualité de service offerte, les solutions logicielles
- mettre en oeuvre dépendent largement des supports de transmission utilisés. Les supports de transmission exploitent les propriétés de conductibilité des métaux (paires torsadées, coaxial…) ou celles des ondes électromagnétiques (faisceau hertzien, fibres optiques, satellite…).
Un support de transmission est essentiellement caractérisé par son impédance
caractéristique et sa bande passante . Ces paramètres conditionnent les possibilités de transmission en termes de débits et de distance franchissable.
1.1) L’impédance caractéristique
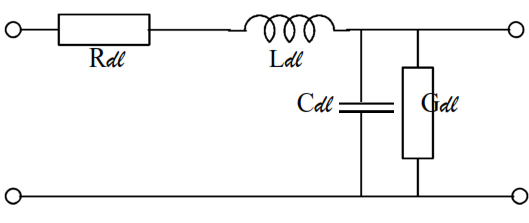
Schéma équivalent d’un élément (dl) d’une ligne de transmission
Une ligne de transmission est constituée de deux conducteurs de cuivre séparés par un isolant. La résistance linéique des conducteurs, la capacité linéique, l’inductance linéique et la conductance linéique sont liés par la relation:
avec ω = 2 × π × f
où ω est la pulsation du courant exprimé en rd/s et f la fréquence du signal en Hertz.
Zc, ou impédance caractéristique, est l’impédance d’une ligne de longueur infinie. On montre qu’une ligne de longueur finie refermée sur un récepteur d’impédance Zr, tel que Zc=Zr, se comporte comme une ligne infinie, on dit alors que la ligne est adaptée (adaptation d’impédance).
Toute rupture d’impédance (Zc≠Zr) provoque une réflexion d’une partie de l’énergie incidente. Cette énergie (onde réfléchie ou écho) se combine à l’énergie incidente pour fournir des ondes stationnaires. pour éviter ces réflexions parasites, il est nécessaire tout au long de la ligne et à chaque raccordement d’un nouvel élément de liaison de réaliser la continuité de l’impédance, c’est l’adaptation d’impédance.
1.2) La bande passante
A l’extrémité de la ligne, le récepteur doit identifier et décoder le signal. Cette fonction ne peut valablement être effectuée que si le signal n’a pas été exagérément modifié pendant la transmission. La bande passante est la grandeur de base qui renseigne sur les possibilités de transmission d’une ligne.
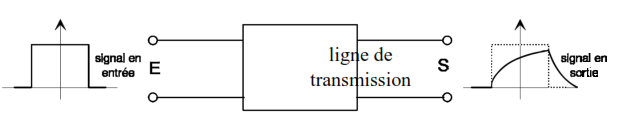une ligne de transmission déforme le signal
2.Notion d’analyse spectrale.
D’après le mathématicien français Joseph FOURIER, une fonction périodique de fréquence f0 peut être considérée comme la somme d’une constante (composante continue) et de fonctions sinusoïdales :
- 3/4 Le fondamentale de fréquence égale à celle du signal périodique ;
- 3/4 Les harmoniques de fréquence multiple à celle du signal périodique.
y(t )=A0 + A1 cos(2πf0 + ϕ1 ) + A2 cos(2π 2 f0 + ϕ 2 ) + … + An cos(2πnf 0 + ϕ n ) A0 représente une constante appelée composante continue
A1 est l’amplitude du signal de même fréquence que le signal d’origine appelé fondamental.
A2…An sont les amplitudes des termes harmoniques de fréquence 2f0 …nf0.
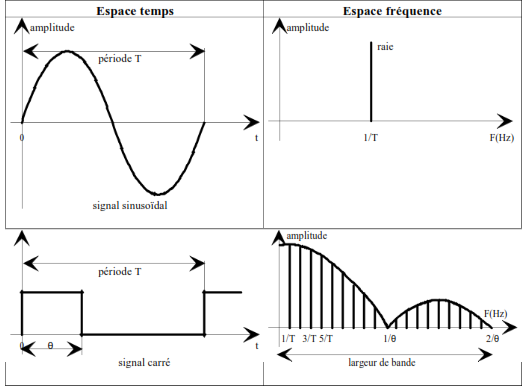
Le tableau de la page suivante représente les décompositions en série de Fourier de différentes fonctions usuelles.
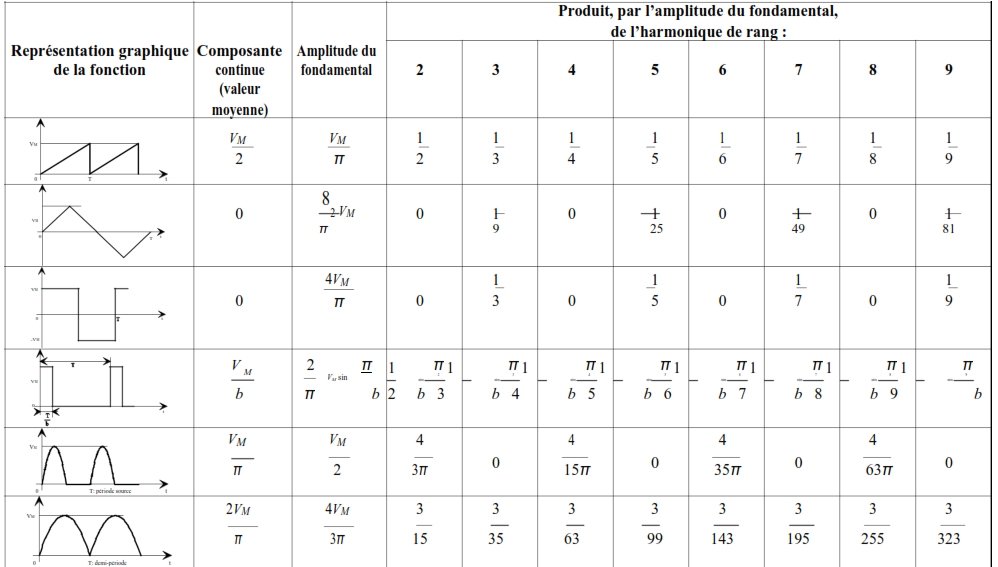Les figures suivantes illustrent la reconstitution d’un signal d’origine à partir de ses composantes. La représentation s’arrête à l’harmonique de rang5. Il faut savoir que plus le nombre d’harmoniques utilisé est important, plus le signal reconstitué est proche du signal d’origine.
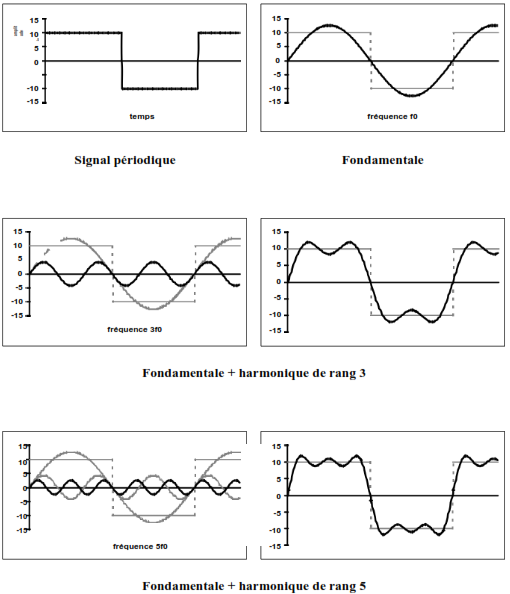Un signal périodique quelconque est constitué d’une infinité de signaux sinusoïdaux. Chaque composante peut être représentée par l’énergie qu’elle contient. Cette représentation est appelée raie de fréquence (transformation de l’espace temps en espace fréquence). L’ensemble des raies de fréquence constitue le spectre de fréquence (spectre de raies) du signal. L’espace de fréquence occupé par le spectre est désigné par le terme de largeur de bande. En théorie, la largeur de bande d’un signal non sinusoïdal est infinie, cependant, dans la pratique, la largeur de bande exprime la largeur du spectre nécessaire à une reconstitution correcte (suffisante pour être interprétée) du signal d’origine.
3. Application à la transmission de données
Les systèmes de transmission (lignes, amplificateurs…) ne transmettent pas toutes les harmoniques du signal de façon identique. Dans ces conditions, le signal en sortie du système n’est plus l’image de celui en entrée, on dit qu’il y a distorsion.
La distorsion est dite en amplitude quand les éléments constitutifs du signal, fondamental et harmoniques, ne sont pas affaiblis de façon identique. La distorsion est dite de phase quand les différents éléments du signal ne sont pas tous transmis dans le même délai. La distorsion d’amplitude est plus importante que la distorsion de phase.
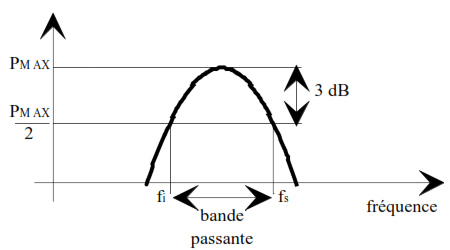
Dans un système de transmission, les signaux sont transmis avec une distorsion faible jusqu’à une certaine fréquence appelée fréquence de coupure. Au-delà de cette fréquence, toutes les harmoniques sont fortement atténuées (filtre passe bas). On appelle bande passante l’espace de fréquence tel que tout signal appartenant à cet intervalle, ne subisse, au plus, qu’un affaiblissement déterminé par rapport à un niveau de référence.
L’affaiblissement, exprimé en décibel (dB), est donné par la relation suivante :
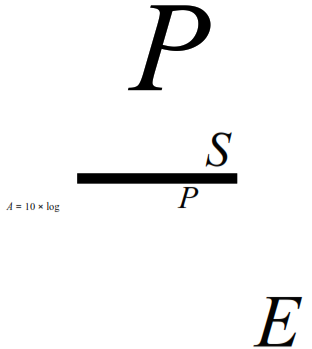PE est la puissance du signal en entrée.
La bande passante est généralement définie à –3 dB, ce qui correspond à une atténuation en puissance de moitié.
4. Notion de rapidité de modulation
Une ligne ou un canal de transmission se comporte comme un filtre passe-bas dont l’un des effets est l’étalement du signal. Dans les conditions limites, cet étalement a pour conséquence que la fin d’une impulsion transmise se confond avec le début de la suivante, les circuits électroniques ne peuvent, alors, distinguer les deux impulsions.
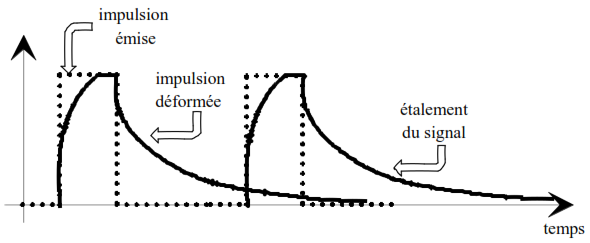Plus la fréquence de coupure haute est faible, plus les impulsions successives devront être espacées dans le temps pour éviter ce phénomène. Le nombre maximal d’impulsions que peut transmettre un système, par unité de temps, est, au plus, égal au nombre de transitions que le système peut admettre.
Si on désigne par te le temps élémentaire ou temps bit (durée du bit), une succession de 0 et 1 constitue un signal périodique de fréquence f et de période T conforme à la représentation suivante :
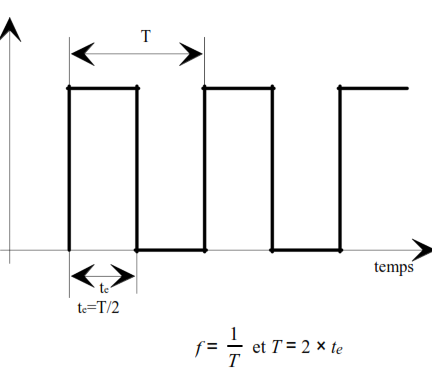Un bit compte pour une demi alternance, dans ces conditions, le temps élémentaire est lié à la fréquence par la relation :
te=T/2 =1/2*f
Si on désigne par R le nombre de temps élémentaire par unité de temps, R et f sont liés par la relation :
R = 1/te = 2 × f
Si fmax est la fréquence de coupure haute du canal, la relation devient :
Rmax = 2 × fmax ou R ≤ 2 × fmax
Si on assimile fmax à la bande passante (BP) du canal, on obtient la relation :
R ≤ 2 × BP
R désigne le nombre maximal de transitions qu’un système peut supporter, et est appelé rapidité de modulation. La rapidité de modulation, grandeur analogue à une fréquence, s’exprime en Baud et représente le nombre de temps élémentaires du signal par unité de temps.
5. Notion de débit binaire et de valence de signal
Le débit binaire d’un canal quantifie la quantité d’information transportée sur le canal par unité de temps, il peut s’exprimer par la relation :
D= 2× BP× log2 n
où n exprime la valence du signal, D est exprimé en bit/s.
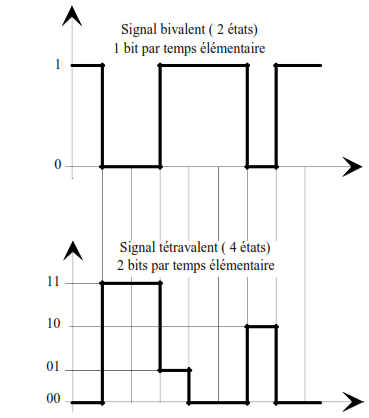
Dans le cas du signal binaire (0,1) la valence du signal est de deux.. Le débit du canal est alors de :
D= 2 × BP × log2 (2) = 2 × BP bit/s
Dans ce cas là, la rapidité de modulation correspond au débit binaire.
Si durant le temps élémentaire, le signal peut prendre plusieurs valeurs, par exemple 4, la valence du signal est alors de quatre. Dans ces conditions, le débit du canal est :
D= 2 × BP × log2 (4) = 4 × BP bit/s
Dans ces conditions, le débit binaire est le double de la rapidité de modulation. C’est ainsi qu’il est possible d’augmenter, sur un canal de transmission de bande passante limitée, le nombre d’informations transmises.
On appelle valence du signal et on la désigne par n, le nombre d’états que peut prendre le signal durant un temps élémentaire. Le débit s’exprime alors par la relation :
D= 2× BP× log2 n
L’opération qui consiste à faire correspondre à un ensemble de symboles binaires (00, 01…) un ensemble de valeurs représentatives (amplitude, fréquence ou phase), durant un intervalle de temps élémentaire, est effectué par un codeur.
En conclusion, rappelons que l’on peut augmenter le débit binaire, sur un canal de transmission donné, en agissant sur :
- La bande passante du canal ;
- Et/ou la valence du signal transporté.
La bande passante est limitée par le système de transmission (support…). On ne peut augmenter indéfiniment le nombre d’états du signal (valence), car les niveaux d’amplitude à discriminer deviennent si faibles qu’ils ne peuvent être distingués du bruit.
6. Notion de bruit
Les signaux transmis sur un canal peuvent être perturbés par des phénomènes électriques ou électromagnétiques désignés sous le terme générique de bruit. On distingue essentiellement deux types de bruit : le bruit blanc et le bruit impulsionnel.
Le bruit blanc provient de l’agitation thermique des électrons. Ses composantes (raies de fréquence) sont également réparties dans le spectre des fréquences, d’où son nom. D’amplitude généralement faible, il est peu gênant pour les transmissions.
Le bruit impulsionnel est une perturbation brève qui à pour origine l’environnement physique du canal de transmission (parasite d’origine électromagnétique). D’intensité élevée et d’apparition erratique, il provoque des erreurs portant sur un ensemble de bits.
Le rapport entre la puissance du signal transmis et celle du signal de bruit qualifie le canal vis à vis du bruit. Ce rapport, appelé rapport signal sur bruit (S/N avec N pour Noise), s’exprime en dB :
Shannon a montré, qu’en milieu perturbé, le nombre maximal d’états discernables (valence) est donné par la relation :
La capacité maximale de transmission d’un canal est donc de :