Blog

Sciences Indusrielles

Automatique : introduction

Cours (1ère partie)

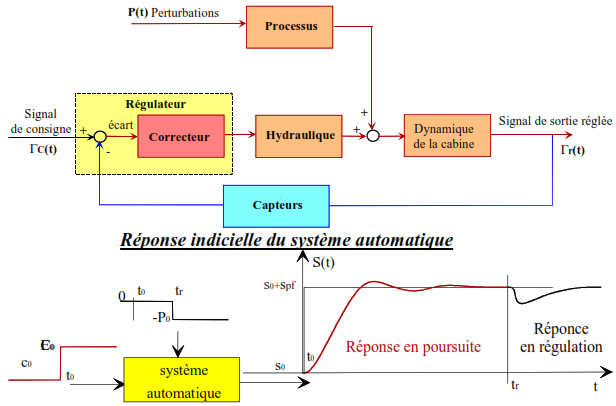
Schéma fonctionnel de l’asservissement

Plan
		**********************
	1   INTRODUCTION ASPECTS GÉNÉRAUX ………………………	2
1.1	généralités sur l’automatique……………………………………………..	2
1.2	Notion de systèmes……………………………………	3
1.3	Rôle de l’automatique …………………………………	5
1.4	Bref historique………………………………………………………………..	7
1.5	Schémas fonctionnels …………………………………………..	9
1.6	Structure d’un système de commande ou système asservi..	11
		**********************

1 INTRODUCTION ASPECTS GÉNÉRAUX

1.1  généralités sur l’automatique

Le substantif « Automatique » a été utilisé pour la première fois en 1914 dans la revue académique royale des sciences de Madrid publié par Torres y Quevedo.

• Le petit Larousse propose la définition suivante :

Automatique : Science et technique de l’automatisation, qui étudient les méthodes scientifiques et lemoyen technologique utilisés pour la conception et la construction des systèmes automatiques.

Automatisation : Exécution automatique de tâches industrielles, administratives ou scientifiques, sansintervention humaine.

L’automatique peut se définir comme un ensemble de théories mathématiques et une technique de raisonnement concernant la prise de décision et la commande des systèmes. La dénomination anglaise est plus explicite ‘Automatique Control » puisqu’elle précise la notion de commande. Le terme anglais « Control » est un faux ami à ne pas traduire comme contrôle, il signifie Commande.

Définition du mot système : Nous le verrons dans d’autre chapitre de cours mais nous pouvons ici retenir une définition littéraire : Un Système consiste en une combinaison de parties qui se coordonnent pour concourir à un résultat.

LES SYSTEMES AUTOMATISES Limites du modèle : Systèmes linéaires continus et invariants partie2

Le but d’un système est d’exécuter des actions qui sont regroupées en a activités. Chaque élément du système assume sa part d’activité. Une action est le résultat de l’organisation de matière, d’énergie et d’information. En quelque sorte, l’information, avec le concours de l’énergie, va modifier la matière en lui conférant un plus grand degré d’organisation.

Des objets agencés entre eux, c’est à dire ayant une certaine dépendance, constituent un système réalisant une certaine fonction ou action.

Les sorties-entrées sont les signaux qui apportent au système, les informations du milieu extérieur. Les sorties fournissent la réponse du système par dépendance des entrées; on peut parler de causes (entrées) et d’effets (sorties).

On utilise de manière synonyme le terme de processus : process en anglais. Théoriquement, un processus se défini comme un ensemble de lois d’évolution de différentes grandeurs physiques, c’est la façon dont évolue un système sous l’effet des entrées. Dans le langage courant, on confond souvent le processus, notion abstraite, et l’installation matérielle dont le fonctionnement est régi par ces lois.

La commande d’un système consiste à exercer, via les entrées, une influence sur le système de manière à obtenir en sortie un comportement déterminé. Cette influence s’exerce souvent par l’intermédiaire d’une action sur le flux d’énergie ou de matériaux injectés dans le système. Lorsque cette influence est exercée par l’Homme, la commande est dite manuelle. Lorsque l’Homme est remplacé par des dispositifs techniques autonomes, on parle de commande automatique.

L’automatique s’est longtemps appliquée qu’aux systèmes mécaniques, électroniques et électromécaniques, mais maintenant elle est utilisée en gestion, biologie, économie, etc.

Les systèmes de commande automatique copient le plus souvent le comportement de l’Homme, Un exemple introductif simple s’obtient par observation d’un conducteur au volant de son véhicule. Le système que l’Homme commande est sa voiture dans un environnement de la route; le cerveau et les membres constituent les organes de commande. Les décisions concernant la direction l’accélération et le freinage sont mises en oeuvre, à partir des mesures effectuées par l’œil, de manière à satisfaire un critère de performance qui peut -être -un compromis entre la durée du trajet, le confort, la consommation ou les réglementations.

Cet exemple nous montre les trois opérations fondamentales accomplies par l’Homme.

• l’observation

• la réflexion
• l’action

Il est intéressant de noter que des types d’actions différentes peuvent être appliqués, suivant les critères intégrés lors de la phase de réflexion. Un conducteur pressé appliquera une succession de freinages et accélérations, au détriment de la consommation alors qu’un autre conducteur économe adoptera une conduite plus souple.

La structure à trois phases met en évidence une opération de bouclage (« Feed-back », nourrir en retour).

Ce retour constitue l’une des notions importantes de l’automatique.

1.2  Notion de systèmes

Un système est un ensemble d’éléments liés entre eux dans le but de réaliser une tâche déterminée. Ce dispositif soumis aux lois physiques est caractérisé par des grandeurs de deux types : Les ENTREES et Les SORTIES.

En général, les entrées et les sorties sont multiples. On définit ses systèmes comme multivariables.

1.2.1     REPRESENTATION D’UN SYSTEME

Les entrées peuvent être classées en deux types :

• Des grandeurs de commandes du système appelées communément Entrées de commandes. Les entrées de commandes correspondent aux signaux que l’on pourra modifier afin d’agir sur le système.

• Des signaux parasites appelés communément Perturbations.

Les perturbations correspondent aux signaux que l’on ne pourra pas manipuler et que le système devra subir.

Par exemple : Pour un four, les grandeurs suivantes peuvent être relevées

• Entrée de commande: Débit de combustible

• Entrée de perturbation déperdition de chaleur

• Sortie : température à l’intérieur du four

Il est devenu maintenant naturel de modéliser un système quelconque. Une représentation graphique de système se représente par un schéma fonctionnel dont on verra la normalisation plus loin dans ce document.

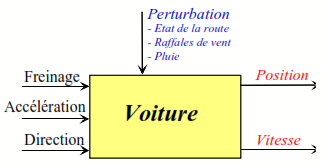
Dans ce schéma fonctionnel sont indiquées les entrées accessibles à la commande, les entrées parasites subies (perturbations), et les sorties intéressantes. Par exemple pour qualifier le comportement d’un véhicule automobile, on dresse une liste sommaire de grandeurs utiles et on précise leur nature avec le schéma ci-contre.

1.2.2      SYSTEME DYNAMIQUE

Un système dynamique est un système dont la réponse dépend simultanément de l’excitation présente et des excitations et réponses passées. Les systèmes qui répercutent instantanément l’effet d’une entrée en sortie, ou sous une autre forme, dont la sortie à un instant ne dépend que de la valeur de l’entrée au même instant, sont dits instantanés.

On se l’imitera dans un premier temps à des systèmes localisés (four, voiture, commande direction de bateau, etc.) dont le comportement est décrit par des équations différentielles ordinaires. Par opposition aux systèmes dits à paramètres distribués ou répartis dont la description du comportement met en oeuvre des phénomènes de propagation (ligne électrique) modélisés par des équations aux dérivées partielles.

Les systèmes réels sont en général des systèmes multivariables (plusieurs entrées-sorties). Cependant, la difficulté de réaliser une commande multidimensionnelle est telle que l’automaticien est incité à sélectionner un couple entrée-sortie conférant ainsi au système une représentation dite monovariable. L’effet des autres entrées ou perturbations est analysé séparément. Si le système subit plusieurs perturbations, on analysera leur effet en ne considérant qu’une seule perturbation présente à la fois puis on superposera les effets (Principe de superposition)

1.2.3     DEMARCHE D’APPROXIMATION D’UN SYSTEME COMPLEXE

Exemple : échangeur de chaleur.

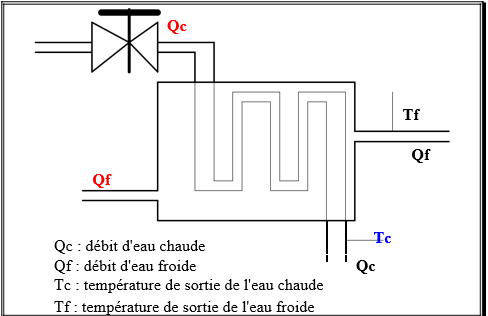
Un échangeur est constitué de deux enceintes dans lesquelles circulent des fluides de températures différentes. La proximité des fluides entraîne des échanges thermiques, permettant ainsi de refroidir ou réchauffer un fluide.

Si la fonction de service de cet échangeur est de refroidir le fluide chaud, Tc est considéré comme grandeur unique de sortie. Il semble évident que les débits Qc et Qf agissent sur cette température. Ce système est donc naturellement multidimensionnel.

L’automaticien pourra retenir comme seule variable d’entrée le débit Qc et considérer en première approximation que Qf est constant. une variation de Qf serait considérée comme une perturbation, d’où le schéma fonctionnel simplifier suivant :

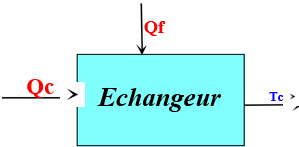
Cet exemple révèle en fait que les grandeurs physiques agissant sur les sorties sont de deux natures :

• Les grandeurs sur lesquelles il est exercé une action volontaire (le débit du fluide chaud réglé par la vanne).

Ces grandeurs seront appelées grandeurs de Commande.

• Les grandeurs laissées libres de leur évolution (le débit du fluide froid pour l’échangeur de chaleur), et cela généralement pour des raisons de coût économique prohibitif ou même, dans certain cas, en raison d’une quasi-impossibilité technique à maîtriser ces variables.

Dans ces conditions, ces grandeurs sont regroupées sous le terme de Perturbations.

Au cours de la synthèse d’un système asservi, on est conduit à donner aux perturbations des caractéristiques particulières du type : perturbation en échelon, en rampe ou parfois de nature aléatoire (bruit). Ces caractéristiques tendent à simuler les allures réelles des signaux auxquels le système est soumis lors de son fonctionnement normal. Parmi ses signaux on a :

• L’échelon (perturbation constante)

• La rampe (perturbation linéaire en fonction du temps)

• La sinusoïde (perturbation sur fréquence)

• Aléatoire, faisant l’objet de traitement probabiliste (perturbation sous forme de bruit)

1.3  Rôle de l’automatique

Il est clair maintenant que réaliser un système automatique, c’est concevoir un système capable d’effectuer une ou plusieurs opérations sans l’intervention de l’homme.

Les systèmes automatiques permettent :

• de réaliser les opérations trop complexes, pénibles ou délicates et ne pouvant être confiées

• l’homme. (Alunissage d’un engin spatial)

• de substituer la machine à l’homme dans des opérations trop répétitives ou dénuées d’intérêt (BDV automatique, appareillage électroménager).

• d’accroître la précision : notion de bouclage

Par exemple un obus tiré par un canon aura un point de chute dans un certain domaine lié aux imperfections et perturbations extérieures. A contrario, un missile téléguidé dont la position ,vitesse et accélération, par rapport à l’objectif sont mesurée à chaque instant atteindra sa cible avec une bien meilleure précision.

• de permettre une action de stabilité. Par exemple, un oscillateur entretenu sera surveillé par un dispositif qui lui évitera de diverger ou de cesser d’osciller.

Il existe deux grands types de système automatiques :

1.3.1     LES SYSTEMES LOGIQUES COMBINATOIRES ET SEQUENTIELS

Les systèmes logiques combinatoires et séquentiels, câbles ou programmés, qui n’ont pas nécessairement une structure bouclée. Cette automatisation porte sur un nombre fini d’opérations prédéterminées dans leur déroulement. Par exemple un programmateur de machine à laver automatique est un tel système.

De tels systèmes sont appelés systèmes à « événement discret » ou « automatismes séquentiels ». Les entrées et les sorties en automatisme séquentiel sont de type booléen (tout ou rien). Cette approche sera abordée en deuxième période.

Exemple : La barrière automatique d’un passage à niveau est un automatisme séquentiel.

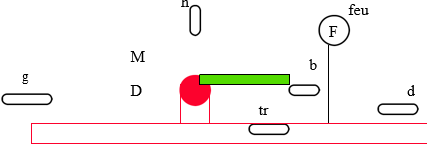
M=1 : moteur de relevage actionné

D=1 : moteur descente actionné

F=1 : Action du feu clignotant

h=1 Barrière relevée	d=1 Arrivée d’un train par la droite
b=1 Barrière baissée	g=1 Arrivée d’un train par la gauche
	tr=1 Train passé

1.3.2     LES SYSTEMES ASSERVIS.

Les systèmes asservis fonctionnent en régulation de maintient ou en poursuite d’une loi de référence. Dans le cas des systèmes asservis, (toutes les situations possibles n’étant pas prévisibles (perturbations)), le déroulement des opérations ne peut être prédéterminé à l’avance. Les systèmes asservis sont nécessairement bouclés, C’est à dire qu’une mesure de la situation est en permanence prise en considération dans la détermination de la commande.

Les entrées et les sorties sont des variables à variation continue en amplitude. Ces systèmes sont appelés système continu ou analogique.

Exemple : La voiture est un système analogique.

Ce système comporte une entrée τ , angle de rotation du volant, et une sortie d, distance du véhicule au bord de la route.

Le système complet de commande comporte une distance d₀ qui fixe la distance désirée (consigne). d₀ n’est pas un signal matérialisé mais une consigne présente dans le cerveau du conducteur. L’angle τ est modifié pour que d soit en permanence égale à d₀, ou tout au moins aussi proche que possible de cette consigne.

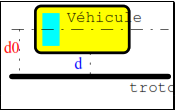
Le schéma fonctionnel se représente sous la forme ci-dessous :

1.4 Bref historique.

Trois époques divisent l’histoire des systèmes automatiques :

1.4.1    LA PREMIERE EPOQUE

Qualifier de préhistoire, elle s’étend de l’antiquité au milieu du siècle dernier. Des inventeurs géniaux ont conçu des systèmes automatiques de manière intuitive.

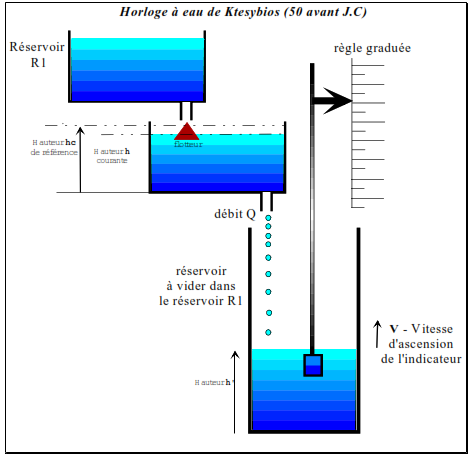
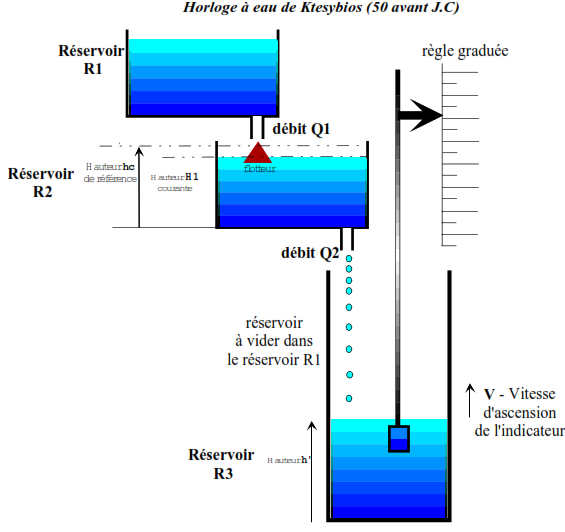
Dès 50 avant J.C, des exemples de régulation de niveau existaient : horloge automatique à eau de Ktesybios (voir figure ci- contre), la lampe à huile de Philon de Byzance et la machine à doser le vin de Héron d’Alexandrie.

hc hauteur de référence pour obtenir le débit voulu en sortie. h hauteur courante dans le réservoir intermédiaire. v vitesse d’ascension de l’indicateur de temps. h’ hauteur d’eau dans le réservoir de sortie.

Le principe de cette horloge est d’animer la tige qui sert d’indicateur avec un mouvement à vitesse constante (amplitude proportionnelle au temps) . Pour obtenir le déplacement on fait varier le volume d’eau d’une manière proportionnelle au temps en utilisant le débit d’alimentation rigoureusement constant. L’intégrale d’un débit constant donne bien un volume variant linéaire ment avec le temps.

Le problème se ramène donc à générer un débit connu constant. Dans un réservoir à écoulement libre, le débit de sortie est en général fonction de la pression, donc de la hauteur d’eau dans le réservoir. Pou obtenir un débit de sortie constant il suffit de garantir un niveau constant.

Le niveau dans le réservoir intermédiaire est contrôlé à cause de une valve liée à un flotteur qui va garantir un niveau de référence.

En fonctionnement normal, cette valve assure un niveau constant égale au niveau de référence souhaité, ce qui implique que le débit corresponde bien à la valeur souhaitée.

Plus tard, Réaumur, Watt et son régulateur de vitesse (1788), Jacquard et son métier à cartes perforées, font progresser l’automatisation.

Le régulateur de Watt a pour but de maintenir constante la vitesse de rotation d’une turbine à vapeur. La commande d’admission de vapeur dans la turbine est contrôlée par une vanne dont on peut manœuvre le pointeau.

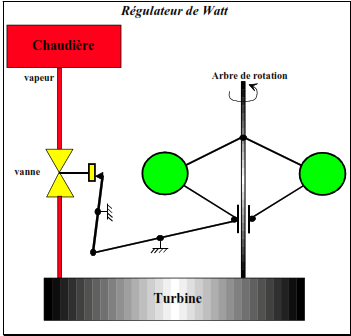
Un ensemble mécanique déformable constitué de masselottes et de tringles permet une mesure de la vitesse de rotation par effet d’inertie. Plus la turbine tourne vite, plus les masselottes sont écartées de l’axe de rotation. Pour réaliser un asservissement en vitesse il suffit de transmettre mécaniquement une variation de cet écartement de commande de déplacement du pointeau de la vanne. Si la vitesse de rotation est trop faible, l’écartement insuffisant des masselottes engendre une ouverture de la vanne d’admission vapeur, entraînant une augmentation de la vitesse. Un comportement symétrique a lieu en cas de vitesse de rotation trop élevée.

1.4.2  LA SECONDE EPOQUE :

Elle débute du milieu du XIX^ème siècle, et est caractérisée par la théorie du bouclage et des applications de l’algèbre de Boole. Les premiers travaux sur le bouclage sont dus à Maxwell (1868); à Routh avec son critère algébrique (1872) et à Hurwitz (1890).

L’étude analytique du régulateur de Watt fut commencée par Maxwell en 1868 et complétée en 1876 par Wichnegradsky. L’étude des systèmes bouclés doit beaucoup à l’approche fréquentielle de Nyquist, Bode, Nichols, Hall, Evans, qui ont laissé leur nom à des représentations et qui ont publié la plupart de leurs résultats à la fin de la seconde guerre mondiale. Les premières implantations des systèmes de commandes à cette époque reposaient sur l’utilisation de dispositif électronique à lampes.

1.4.3     LA TROISIEME EPOQUE :

Elle débute dans les années cinquante. L’apparition de calculateurs numériques révolutionne le monde de l’automatique. La puissance de calcul disponible fait naître les méthodes dites de l’automatique moderne ou avancée. Parmi les faits marquant, on peut citer :

• Introduction de la représentation d’état, particulièrement bien adaptée à l’utilisation des calculateurs numériques pour l’étude et la commande des systèmes complexes et multivariables. (Kalman 1960).

• Développement des méthodes d’étude des systèmes non-linéaires (Kochenburger, Cypkin) et des systèmes échantillonnés (Jury, Ragazzini).
• Prise en compte des phénomènes aléatoires dans les théories récentes comme celles de Kalman

et De Bucy.

1.5 Schémas fonctionnels

1.5.1     SYNTAXE DES SCHEMAS FONCTIONNELS

Le recours à un schéma est naturel dans la plupart des techniques, à tel point que cela fait l’objet de symboles normalisés.

Un schéma fonctionnel consiste en une représentation graphique abrégée des relations de cause à effet entre le signal d’entrée et le signal de sortie d’un système de commande.

Définition : Un système de commande est un assemblage de constituants physiques branchés ou reliés les uns les autres de telle sorte qu’il puisse se commander, se diriger ou se régler lui-même, ou bien commander, diriger ou régler un autre système.

C’est un moyen à la fois utile et aisé de caractériser les relations fonctionnelles existant entre les différents organes d’un système de commande.

On peut également utiliser le terme élément pour désigner un organe du système.

Le schéma fonctionnel le plus simple est constitué d’un seul élément avec un signal d’entrée et un signal de sortie comme le montre la figure ci- dessous.

On inscrit à l’intérieur du rectangle représentant l’élément , la description ou le nom de l’organe ainsi que le symbole de l’opérateur mathématique à effectuer sur le signal d’entrée pour obtenir le signal de sortie.

Les flèches indiquent le sens dans lequel l’information et le signal se transmettent.

On représente les opérations d’addition et soustraction d’une manière particulière. L’élément est figuré par un petit cercle, appelé Comparateur où aboutissent des flèches portant le signe + ou – selon les cas. Le signal de sortie est constitué par la somme algébrique des signaux d’entrée. On peut faire aboutir au même comparateur un nombre quelconque de signaux d’entrée.

Certains auteurs marquent le cercle d’une croix :

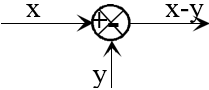
On appelle Point de Dérivation le point où l’on prélève un signal à destination de plusieurs organes d’un système de commande.

1.5.2 EXEMPLE DE SCHEMA FONCTIONNEL EN FONCTION DU SYSTEME ISOLE

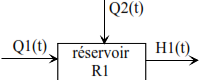
• Schéma fonctionnel du réservoir R2 seul non considéré dans l’environnement présenté ci-dessus Le réservoir R2 alimenté par un débit d’entrée Q1(t) et dont on observe la hauteur H1(t) pour sortie peut être représenté par le schéma fonctionnel simple :

Analysons maintenant le réservoir R2 dans sont environnement

• Schéma fonctionnel du réservoir R2 seul considéré dans l’environnement présenté ci-dessus

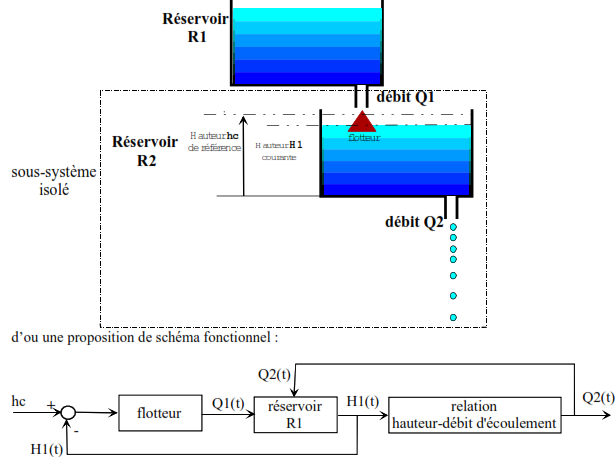
1.6 Structure d’un système de commande ou système asservi.

1.6.1 COMMENTAIRE RAPIDE SUR LA MODELISATION DES SYSTEMES

Robert VALLEE (contemporain en bonne santé) nous donne une bonne définition de la modélisation des systèmes, que nous pouvons prendre à notre compte.

• Le but de la modélisation est de fournir une image ou une représentation d’un phénomène réel. S’il est possible, à partir de la représentation de retrouver parfaitement le phénomène dans son évolution, il y a isomorphisme. Il est évident que ce cas extrême n’est jamais réalisé. Dans le cas général, l y a dégradation dans

le passage à la représentation et finalement simplement homomorphisme (dans le meilleur des cas). Mais il n’y a pas là un défaut. Si selon KORZYBSKI, la carte n’est pas le territoire, c’est un avantage car la carte est alors exemple de détails inutiles non pertinents. L’idée d’utilité apparaît ainsi naturellement. L’utilité d’une modélisation se mesure en fonction du but visé. Il y a des modélisations faites pour aider à comprendre, elles doivent être relativement simples, et d’autres pour aider à agir, elles peuvent accepter une plus grande complexité. »

Nous ajouterons, en guise d’avertissement, la citation d’un auteur inconnu.

 » L’esprit limite sa perception des choses à ce qu’il peut concevoir et il appelle cela la Réalité. »

1.6.2    UNE DEMARCHE DE MODELISATION

1-         Isoler le système à étudier.

Pour cela il faut parfaitement définir les limites du système, puis remplacer son environnement par un ensemble de relations d’entrées-sorties ayant des relations d’équivalentes

2- Effectuer une décomposition en sous systèmes couplés par des relations. Pour chaque sous système, ilfaudra les isoler parfaitement. Les frontières de découpage passent en général par des points de rupture des caractéristiques que l’on observe (Structures matérielles discontinues dans l’espace, dans le temps, au niveau des fonctionnalités.) De la finesse du découpage dépend la connaissance recherchée plus ou moins poussée du système à étudier.

3- Etablir un modèle de connaissance ou de comportement pour chaque sous-système.

1.6.3 BOUCLAGE, REGULATION, ET ASSERVISSEMENT.

Un bouclage apparaît chaque fois au cours d’une opération. Un système prend en compte l’observation de son état pour la modifier

Exemples de système bouclé :

• Régulation de température d’un fer à repasser pendant l’opération de repassage. (système automatique)

• Automobile et pilote réalisant une opération de conduite(système non automatique)

Le bouclage est nécessaire dans les opérations où :

• La précision mise en jeu est importante. L’observation de la grandeur à asservir permet deconstater un écart ou une dérive quelconque par rapport à la référence (ou consigne) souhaitée et donc de réagir en conséquence. Dans une solution sans bouclage, on est amené à faire a priori des hypothèses quant au comportement de certains éléments, toute variation par rapport au comportement de certains composants présupposé entraîne irrémédiablement un défaut sur le résultat final. On remarque ici que la précision du résultat final dépend essentiellement de la précision avec laquelle est faite l’observation.

• Des perturbations interviennent en cours d’opérations modifiant ainsi l’état du système. Parexemple, l’ouverture de la porte d’un four thermostaté entraîne une déperdition de chaleur et donc une baisse de température que l’on compense en augmentant la puissance de chauffage. Dans le cas d’un système bouclé, l’observation de la grandeur de sortie rendra compte de l’apparition d’une perturbation.

• Le comportement du système est mal connu ou variable.

• La stabilité est en cause. Soit que l’on souhaite stabiliser u système naturellement divergent,soit l’on souhaite améliorer un comportement dynamique insatisfaisant. (Attention, le bouclage d’un système naturellement stable le déstabilise toujours un peu)

Ces différents besoins peuvent naturellement coexister dans certaines opérations. Parmi les classes de systèmes asservis on distingue :

• Les régulations qui sont des systèmes destinés à maintenir une ou plusieurs grandeurs physiques à des valeurs fixées constantes, même en présence de perturbations.

Exemples : régulation de vitesse (régulateur de Watt), pilote automatique d’avion (maintient d’attitude et d’altitude malgré les perturbations)

• Les asservissements qui sont des systèmes destinés à faire suivre une loi généralement non fixée à l’avance à une ou plusieurs grandeurs physiques. Dans ce cas, l’asservissement a pour mission d’assurer une recopie la plus fidèle possible quelles que soient les lois de variations fixées. Les asservissements font souvent intervenir les organes mécaniques. On parle alors de servomécanismes.

Par exemple, un pilote automatique d’un engin mobile ou une commande numérique de machine outil réalisent des asservissements.

1.6.4     SCHEMA FONCTIONNEL D’UN SYSTEME DE COMMANDE OU ASSERVI.

On relie entre eux les éléments représentant les différents organes d’un système de commande de façon à caractériser leurs rapports fonctionnels au sein de l’ensemble. Le schéma fonctionnel ci-dessous illustre la structure de base d’un système de commande élémentaire en boucle fermée (à retour).

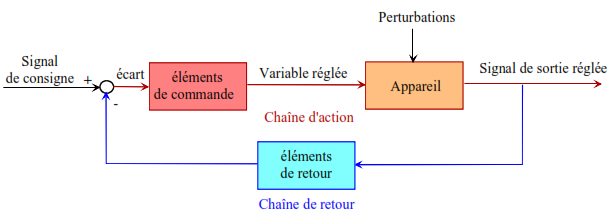
Il est nécessaire de bien comprendre que les flèches de la boucle fermée qui relient les éléments les uns aux autres, représentent la circulation de l’énergie nécessaire à l’asservissement (à la commande), ou l’information, et non la principale source d’énergie du système.

Par exemple, la principale source d’énergie d’un four à thermostat peut être classique et provenir de la combustion du charbon et du fuel. Mais ce n’est pas cette source d’énergie qui apparaît dans la boucle d’asservissement (fermée) du système.

1.6.4.1  Terminologie

Il est important de bien se rappeler les termes dont on se sert dans les schémas fonctionnels en boucles fermées.

On utilise des lettres minuscules pour représenter les variables d’entrées et de sorties de chaques élément ainsi que pour désigner chaque élément g1, g2 et h. Ces quantités sont fonction du temps sauf indication contraire.

On utilise les lettres majuscules pour désigner les transformées de Laplace développées dans un prochain chapitre.

1.6.4.2  Définitions

• On appelle appareil ou processus g2 le système, le sous-système ou l’opération placé(e) sous asservissement, au moyen d’un moyen d’un dispositif de contrôle.

• On appelle signal de sortie réglée c la grandeur produite par l’appareil sous asservissement au moyen d’un dispositif de contrôle.
• On appelle chaîne d’action l’ensemble des éléments placés entre le point de sommation et la sortie

réglée.

• On appelle organes de commande g1 les éléments de la chaîne d’action qui engendrent le signal de commande u et m fourni par l’appareil.

Les organes de commande sont en général des régulateurs, des correcteurs, des égaliseurs et/ou des amplificateurs.

• On appelle signal de commande u (ou grandeur réglée m) le signal de sortie délivré par les organes de commandes g1 à l’appareil g2.

• On appelle chaîne de retour l’ensemble des éléments situés entre la sortie réglée c et le point de sommation.

• On appelle organe de retour h les éléments de la chaîne de retour établissant une relation entre la sotie réglée c et le signal de retour b.

Les organes de retour sont en général des capteurs de mesure de la sortie réglée c, des correcteurs et/u des régulateurs.

• On appelle signal de référence ou valeur de consigne r un signal externe fourni au système asservi, en général sur le sommateur, pour obtenir une réponse déterminée de l’appareil sous contrôle. Sa valeur correspond au fonctionnement optimal ou désiré de l’appareil.

• On appelle signal de retour primaire b une fonction de l sortie réglée c fournie par la chaîne de retour, que l’on somme algébriquement avec la référence r pour obtenir un signal d’erreur e.

Ce signal n’existe pas en boucle ouverte.

• On parle de retour positif lorsque le sommateur est un additionneur, c’est à dire e = r+b et de retour négatif ou contre réaction lorsque le sommateur est un soustracteur soit e = r-b.

1.6.5     STRUCTURE D’UN SYSTEME ASSERVI OU BOUCLE

Trois fonctions essentielles gèrent la réalisation d’un système asservi ou bouclé :

1. L’OBSERVATION

• La REFLEXION (dans le cadre d’un opérateur humain) ou TRAITEMENT ALGORITHMIQUE (par un système électronique ou informatique)
• L’ACTION.

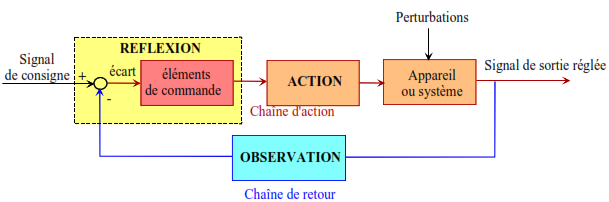
Suivant les réalisations, ces trois opérations sont exécutées simultanément ou successivement.

Explicitons ces trois opérations à propos d’un exemple. Prenons pour tâche de réaliser le remplissage d’une cuve dont on souhaite maintenir le niveau à une hauteur de consigne donnée. Dans ce cas, les trois opérations sont les suivantes :

1. Observation du niveau d’eau dans la cuve,

• Comparaison avec le niveau de consigne

• Action sur le robinet (ouverture ou fermeture)

Représentation générale d’un système automatique sous forme de schéma fonctionnel. Ce schéma fonctionnel est la représentation générique d’un système automatique bouclé.

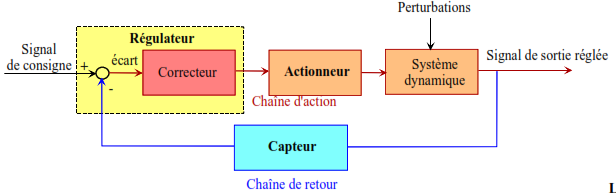
régulateur (comparateur et correcteur) élabore l’ordre de commande de l’actionneur à partir de la consigne et dela mesure. C’est l’organe intelligent. Dans la pratique, le régulateur est en général réalisé par un dispositif électronique ou par un calculateur numérique.

L’actionneur ou l’organe d’action apporte, en général, la puissance nécessaire à la réalisation de latâche : c’est l’organe musclé (vanne, moteur).

Le système dynamique évolue suivant les lois physiques (thermodynamique, mécanique, mécanique desfluides, chimique de réaction, etc.) qui lui sont propres. La sortie ou grandeur réglée est, en générale, une grandeur physique que l’on considère comme importante dans la tâche à réaliser. De plus, cette sortie peut fluctuer en fonction de perturbations extérieures souvent imprévisibles.

Le capteur délivre à partir de la sortie une grandeur caractérisant l’observation. Sa principale qualité estla précision dont dépendra la précision du système global. Il doit fournir une information quasi instantanée par rapport aux évolutions temporelles de la sortie.

1.6.6     QUALITES D’UN ASSERVISSEMENT.

L’étude d’un système asservi consiste à déterminer sa réponse y(t) à une entrée fonction du temps x(t) donnée.

Pour caractériser les performances du système, on se place le plus souvent dans les conditions suivantes:

L’entrée x(t) est l’une des fonctions du temps précisées ci-dessous :

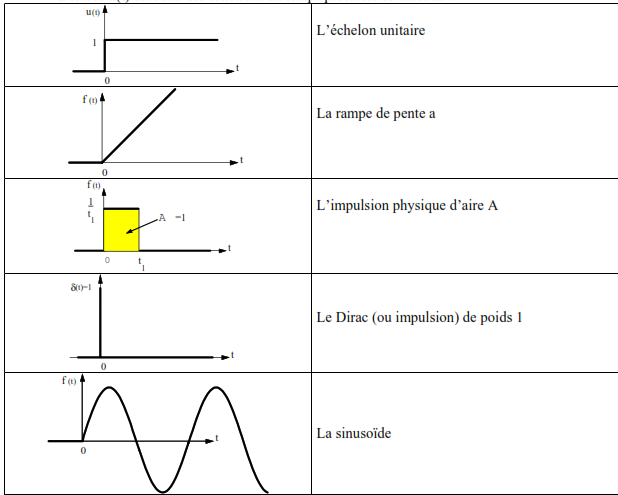
Pour tenir compte des discontinuités, on distingue l’instant t = 0- et l’instant 0+.

La sortie y(t) et ses dérivées par rapport au temps sont supposées nulles pour les instants : t<O- : On dira que le système est initialement au repos.

Dans ces conditions, la réponse y(t) comporte en général un régime transitoire et un régime établi ou régime permanent (obtenu pour t suffisamment grand). Voir figure ci-dessous.

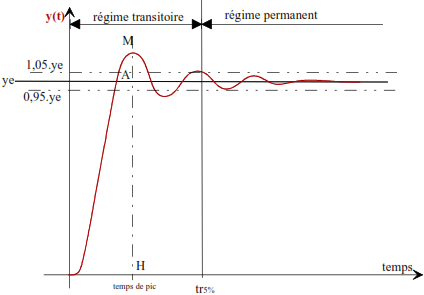
Exemple de réponse indicielle (réponse à un échelon d’un système initialement au repos)

Le régime transitoire est caractérisé essentiellement par :

• Le dépassement D : D = AM / HA, en général, le dépassement est exprimé en pourcentage.

• Le temps de réponse tr (durée du régime transitoire). Par exemple, pour un critère à 5%, le temps de réponse à 5% est le temps au-delà duquel l’écart relatif entre y(t) et ye (régime établi) est inférieur à 5%.

En général pour les servomécanismes, il est souhaité un régime transitoire de courte durée et à faible dépassement

1.6.6.1  L’aspect dynamique – L’aspect statique

Dans l’analyse des systèmes asservis, nous distinguons donc l’aspect statique de l’aspect dynamique.

L’aspect statique concerne l’étude des systèmes asservis en régime permanent (entrée fixe). On définitl’erreur statique comme étant la différence entre la sortie demandée (consigne) et la sortie réalisée lorsque que le régime d’équilibre est établi (c’est à dire pour t grand). Au cours de la conception des systèmes asservis, on s’efforcera en général d’annuler cette erreur.

L’aspect dynamique, essentiellement en automatique, s’étudie par les notions de précision dynamique,de rapidité et de stabilité. (il est à noter qu’à l’heure d’aujourd’hui, la précision dynamique des systèmes automatisés n’est pas au programme de C.P.G.E.). Il s’intéresse au comportement transitoire de la sortie, soit suite à une variation de la consigne, soit suite à l’apparition d’une perturbation dans la chaîne fonctionnelle.

1.6.7     LES PERFORMANCES D’UN ASSERVISSEMENT

1.6.7.1  Les quatre critères de performance

• La stabilité :   absence de divergence entre la valeur de sortie et la valeur visée.

La stabilité est la performance nécessaire des servomécanismes. Sans stabilité pas d’étude. Elle se

caractérise par son degré, qui peut être quantifié par le dépassement, ou l’amortissement, ou par la marge de gain, ou la marge de phase.

Le réglage du degré de stabilité d’un asservissement est souvent la première étude à mener lors d’une analyse ou dune conception d’un système automatisé. C’est en agissant sur le régulateur et plus précisément sur le correcteur que les réglables du degré de stabilité sont effectués.

Remarque : Le choix d’un degré de stabilité influe forcement sur la rapidité

L’étude en régime permanent permet de caractériser :

•     La précision statique (t tend vers l’infini): mesurée par l’écart entre la valeur de sortie et la valeurvisée.

L’étude du régime transitoire permet de caractériser :

• La rapidité : mesurée par le temps de réponse au bout duquel la valeur de sortie reste dans unefourchette exprimée en pourcentage (souvent 5 %) centrée sur la valeur visée. Le temps de réaction d’un processus est étroitement lié à son inertie. (très liée au degré de stabilité)

• L’amortissement : caractérisé par le rapport entre les amplitudes successives des oscillations de lavaleur de sortie (très lié au degré de stabilité)

• précision dynamique (régime transitoire) (hors programme en C.P.G.E.)

1.6.7.1.1 L’asservissement idéal

En manière de systèmes de commande comme ailleurs il n’y a pas de critère absolu, il n’y a que des critères relatifs à des problèmes précis. C’est en ayant présent à l’esprit cette réserve fondamentale qu’il convient de lire ce qui suit.

On recherche une bonne stabilité et une bonne précision, mais le régime transitoire doit être rapide et bien amorti.

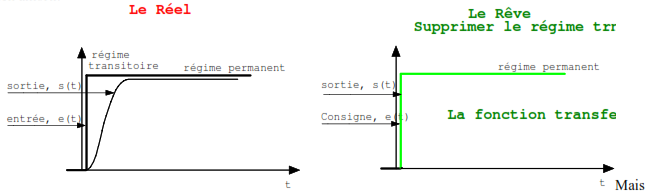
Si le régime transitoire était nul, quel plaisir. On donne un ordre à un système et Hop !!???, il est immédiatement réalisé. Sûrement trop facile et donc ennuyeux.

Nous verrons par la suite, pourquoi le fait de ne pas savoir aujourd’hui, fabriquer et concrétiser un dérivateur pure nous empêche d’obtenir instantanément notre demande (la consigne), mais heureusement, cela ne nous empêche pas de rêver.

1.6.7.1.2 Dilemme rapidité-amortissement ou degré de stabilité.

Dilemme stabilité-précision

Ces critères de performance ne sont pas toujours compatibles et nous conduisent souvent à des compromis qui font le plaisir de l’automatisme. La solution unique n’existant pas, il est donc nécessaire de mettre en place des critères d’évaluation et de choix de solutions.

Par exemple en mécanique un processus rapide est léger, il a ainsi faible inertie, il risque donc d’être peu amorti voire instable.

D’autre part si on veut améliorer la précision on raidit l’asservissement mais on risque de tomber alors sur le phénomène de pompage mais si on cherche à être tranquille du côté de la stabilité on risque de réaliser un asservissement mou et peu précis.

1.6.7.1.3 Stabilité

La stabilité traduit la propriété de convergence temporelle asymptotique vers un état d’équilibre. Un système stable peut en effet présenter une sortie divergente soit en raison du comportement dynamique intrinsèque de système commandé, soit en raison d’un bouclage. Ce comportement instable est intolérable pour un système asservi. Il sera donc souvent exiger un comportement transitoire correctement amorti (le correctement est difficile à définir).

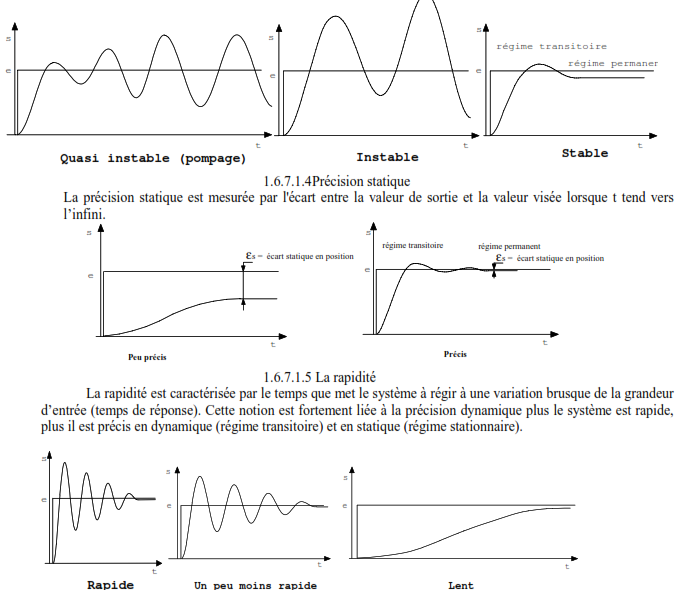
la rapidité d’un système est quantifiée par le temps de réponse affecté d’un critère sous égal à 5%. tr5% est déterminé à partir de l’instant pour lequel la valeur instantanée de la sortie s(t) est à une distance inférieure à 5% de la valeur finale (ici K). (voir figure ci-dessous)

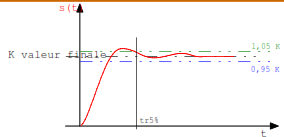
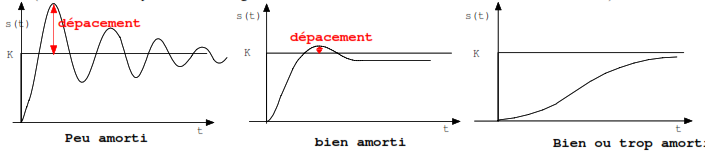
1.6.7.1.6 L’amortissement ou degré de stabilité

L’amortissement permet de quantifier le degré de stabilité d’un système. Plus il est grand, plus le système est amorti.

Il est à remarquer que plus le système est amorti moins il est rapide ; et si le système est trop peu amorti sont temps de réponse à 5% grandi. Il est donc nécessaire, comme toujours de trouver le bon compromis.

Le dépassement est lui aussi important et peu être en fonction des cas (cahier de charges) autorisé ou non. (là encore les compromis sont de rigueur et les critères de choix doivent être clairement identifiés)

1.6.7.1.7 La qualité d’un système automatique

Le cahier des charges de tout système bouclé s’énonce en trois points : Stabilité, Rapidité de réponse, Précision. La qualité du système dépend donc de ses trois points.

Conclusion :

La structure bouclée, la possibilité de trouver des lois de commande convenables et même parfois assez sophistiquées, permettent de créer automatiquement la commande appropriée. Les contraintes du cahier des charges sont nombreuses et contradictoires ; s’y ajoutent parfois des exigences nouvelles : Économie d’énergie, économie du matériel, qu’il faut prendre en compte (une voiture qui démarre vite use prématurément ses pneus). La synthèse d’une commande automatique résulte, avant tout, de compromis.

Telecharger